题目内容
 如图所示,测量人员在山脚A处测得山顶B的仰角为35°,沿着坡脚为20°的斜坡走了1000m到达S处,在S处测得山顶B的仰角为65°,求山的高度.
如图所示,测量人员在山脚A处测得山顶B的仰角为35°,沿着坡脚为20°的斜坡走了1000m到达S处,在S处测得山顶B的仰角为65°,求山的高度.考点:解三角形的实际应用
专题:应用题,解三角形
分析:先利用正弦定理,求出BS,再计算BE,CE,即可得出结论.
解答:
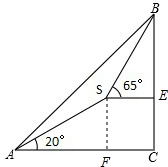 解:∵∠BAC=35°,∠SAC=20°,
解:∵∠BAC=35°,∠SAC=20°,
∴∠BAS=15°,
∵∠BSE=65°,∠BES=90°,
∴∠SBE=25°,
∵∠ABC=55°,
∴∠ABS=30°,
∴AS=1000,
∴BS=
=500(
-
),
∴BE=BSsin65°=500(
-
)sin65°,
过点S作SF⊥AC,则SF=ASsin20°=1000sin20°
∴BC=500(
-
)sin65°+1000sin20°米.
 解:∵∠BAC=35°,∠SAC=20°,
解:∵∠BAC=35°,∠SAC=20°,∴∠BAS=15°,
∵∠BSE=65°,∠BES=90°,
∴∠SBE=25°,
∵∠ABC=55°,
∴∠ABS=30°,
∴AS=1000,
∴BS=
| 1000sin15° |
| sin30° |
| 6 |
| 2 |
∴BE=BSsin65°=500(
| 6 |
| 2 |
过点S作SF⊥AC,则SF=ASsin20°=1000sin20°
∴BC=500(
| 6 |
| 2 |
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
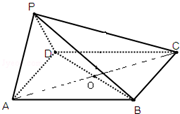 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=