题目内容
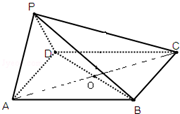 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(1)求证:面PAB⊥平面PDC;
(2)求点O到面PAB的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:
分析:(1)先证明CD⊥平面PAD,所以CD⊥PA,再证明PA⊥PD,可得PA⊥面PDC,即可证明面PAB⊥平面PDC;
(2)证明PD⊥面PAB,可得点D到面PAB的距离为|PD|,即可求点O到面PAB的距离.
(2)证明PD⊥面PAB,可得点D到面PAB的距离为|PD|,即可求点O到面PAB的距离.
解答:
 (1)证明:因为面PAD⊥面ABCD,平面PAD∩面ABCD=AD,ABCD为正方形,
(1)证明:因为面PAD⊥面ABCD,平面PAD∩面ABCD=AD,ABCD为正方形,
所以CD⊥AD,CD?平面ABCD,
所以CD⊥平面PAD,
所以CD⊥PA,
又PA=PD=
AD,
所以△PAD是等腰直角三角形,且∠PAD=
,
即PA⊥PD,
因为CD∩PD=D,且CD、PD?面ABCD,
所以PA⊥面PDC,
又PA?面PAB,
所以面PAB⊥面PDC;
(2)解:因为PA=PD=
a,AD=a,所以PD⊥PA
因为面PAD⊥底面ABCD交线为AD,AB⊥AD,AB?面ABCD
所以AB⊥面PAD,所以有AB⊥PD,
因为PA∩AB=A,
所以PD⊥面PAB,即点D到面PAB的距离为|PD|
又因为O为线段BD的中点,所以点O到面PAB的距离为
=
a.
 (1)证明:因为面PAD⊥面ABCD,平面PAD∩面ABCD=AD,ABCD为正方形,
(1)证明:因为面PAD⊥面ABCD,平面PAD∩面ABCD=AD,ABCD为正方形,所以CD⊥AD,CD?平面ABCD,
所以CD⊥平面PAD,
所以CD⊥PA,
又PA=PD=
| ||
| 2 |
所以△PAD是等腰直角三角形,且∠PAD=
| π |
| 2 |
即PA⊥PD,
因为CD∩PD=D,且CD、PD?面ABCD,
所以PA⊥面PDC,
又PA?面PAB,
所以面PAB⊥面PDC;
(2)解:因为PA=PD=
| ||
| 2 |
因为面PAD⊥底面ABCD交线为AD,AB⊥AD,AB?面ABCD
所以AB⊥面PAD,所以有AB⊥PD,
因为PA∩AB=A,
所以PD⊥面PAB,即点D到面PAB的距离为|PD|
又因为O为线段BD的中点,所以点O到面PAB的距离为
| |PD| |
| 2 |
| ||
| 4 |
点评:本题考查面面垂直,考查线面垂直,考查点到平面距离,考查学生分析解决问题的能力,正确运用面面垂直的判定定理是关键.

练习册系列答案
相关题目
“a<b”是“log2a<log2b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图所示,测量人员在山脚A处测得山顶B的仰角为35°,沿着坡脚为20°的斜坡走了1000m到达S处,在S处测得山顶B的仰角为65°,求山的高度.
如图所示,测量人员在山脚A处测得山顶B的仰角为35°,沿着坡脚为20°的斜坡走了1000m到达S处,在S处测得山顶B的仰角为65°,求山的高度.