题目内容
已知函数f(x)=x3+ax2-x+c(x∈R),下列结论错误的是( )
| A、函数f(x)一定存在极大值和极小值 | ||||
B、若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥
| ||||
| C、函数f(x)的图象是中心对称图形 | ||||
| D、函数f(x)一定存在三个零点 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:先求出函数的导数,找到单调区间,列出表格,逐一排除,得出答案.
解答:
解:∵f′(x)=3x2+2ax-1.
∴△=4a2+12>0,
∴f′(x)=0有两解,不妨设为x1<x2,列表如下
由表格可知:
①x=x1时,函数f(x)取到极大值,x=x2时,函数f(x)取到极小值,故选项A正确,
②函数f(x)在(-∞,x1),(x2,+∞)上是增函数,x2-x1=
=
≥
,故选项B正确,
③∵f(-
a-x)+f(x)=
+
,f(-
)=
+
,∴f(-
-x)+f(x)=2f(-
),∴(-
,f(-
))为对称中心,故选项C正确,
选项A,B,C都正确,利用排除法,选项D错误,
故选:D.
∴△=4a2+12>0,
∴f′(x)=0有两解,不妨设为x1<x2,列表如下
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
①x=x1时,函数f(x)取到极大值,x=x2时,函数f(x)取到极小值,故选项A正确,
②函数f(x)在(-∞,x1),(x2,+∞)上是增函数,x2-x1=
| (x1+x2)2-4x1x2 |
2
| ||
| 3 |
2
| ||
| 3 |
③∵f(-
| 2 |
| 3 |
| 4a3 |
| 9 |
| 2a |
| 3 |
| a |
| 3 |
| 2a3 |
| 9 |
| a |
| 3 |
| 2a |
| 3 |
| a |
| 3 |
| a |
| 3 |
| a |
| 3 |
选项A,B,C都正确,利用排除法,选项D错误,
故选:D.
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,是一道综合题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知命题“p:x≥4或x≤0”,命题“q:x∈Z”,如果“p且q”与“非q”同时为假命题,则满足条件的x为( )
| A、{x|x≥3或x≤-1,x∉Z} |
| B、{x|-1≤x≤3,x∉Z} |
| C、{-1,0,1,2,3} |
| D、{1,2,3} |
设函数f(x)=
,类比课本推导等差数列前n项和公式的推导方法计算f(-4)+f(-3)+…+f(0)+f(1)+…+f(4)+f(5)的值为( )
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),那么数列{an}的前50项和S50的最小值为( )
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
函数f(x)=x3-ax在(-∞,1]上递增,则a的范围是( )
| A、a>3 | B、a≥3 |
| C、a<3 | D、a≤3 |
等差数列{an}中,a3+a7=15,则a2+a8=( )
| A、10 | B、15 | C、12 | D、8 |
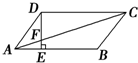 如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )
如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )| A、54cm2 |
| B、24cm2 |
| C、18cm2 |
| D、12cm2 |