题目内容
已知抛物线x2=2py（p＞0）的焦点为F，过F作倾斜角为300的直线，与抛物线交于A，B两点，若|AF|＜|BF|，则
=（ ）
| |AF| |
| |BF| |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：作AA1⊥x轴，BB1⊥x轴．则可知AA1∥OF∥BB1，根据比例线段的性质可知
=||
=
，根据抛物线的焦点和直线的倾斜角可表示出直线的方程，与抛物线方程联立消去x，根据韦达定理求得xA+xB和xAxB的表达式，进而可求得xAxB=-（
）2，整理后两边同除以xB2得关于
的一元二次方程，求得
的值，进而求
．
| |AF| |
| |FB| |
| |OA1| |
| |oB1| |
| |xA| |
| |XB| |
| xA+xB | ||||
|
| xA |
| xB |
| xA |
| xB |
| |AF| |
| |FB| |
解答：
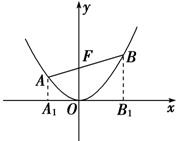解：如图，作AA1⊥x轴，
BB1⊥x轴．
则AA1∥OF∥BB1，
∴的性质可知
=||
=
，
又已知xA＜0，xB＞0，
∴
=-
，
∵直线AB方程为y=xtan30°+
，即y=
x+
，
与x2=2py联立得x2-
px-p2=0
∴xA+xB=
p，xA•xB=-p2，
∴xAxB=-p2=-（
）2，
=-
（xA2+xB2+2xAxB）
∴3xA2+3xB2+10xAxB=0
两边同除以xB2（xB2≠0）得
3（
）2+10
+3=0
∴
=-3或-
．
又∵xA+xB=
p＞0，
∴xA＞-xB，
∴
＞-1，
∴
=-
=-（-
）=
，
故选：B．
解：如图，作AA1⊥x轴，BB1⊥x轴．
则AA1∥OF∥BB1，
∴的性质可知
| |AF| |
| |FB| |
| |OA1| |
| |oB1| |
| |xA| |
| |XB| |
又已知xA＜0，xB＞0，
∴
| |AF| |
| |FB| |
| xA |
| xB |
∵直线AB方程为y=xtan30°+
| p |
| 2 |
| ||
| 3 |
| p |
| 2 |
与x2=2py联立得x2-
2
| ||
| 3 |
∴xA+xB=
2
| ||
| 3 |
∴xAxB=-p2=-（
| xA+xB | ||||
|
=-
| 3 |
| 4 |
∴3xA2+3xB2+10xAxB=0
两边同除以xB2（xB2≠0）得
3（
| xA |
| xB |
| xA |
| xB |
∴
| xA |
| xB |
| 1 |
| 3 |
又∵xA+xB=
2
| ||
| 3 |
∴xA＞-xB，
∴
| xA |
| xB |
∴
| |AF| |
| |FB| |
| xA |
| xB |
| 1 |
| 3 |
| 1 |
| 3 |
故选：B．
点评：本题主要考查了抛物线的性质，直线与抛物线的关系以及比例线段的知识．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
