题目内容
用符号[x)表示超过x的最小整数,如[3.9)=4,[-1.08)=-1.有下列命题:
①若函数f(x)=[x)-x,x∈R,则值域为(0,1];
②若x,y∈{
,3,
},则[x)•[y)=3的概率为
;
③若x∈(1,4),则方程若[x)-x=
有三个根;
④如果数列{an}是等比数列,n∈N*,那么数列{[an)}一定不是等比数列.
其中正确的是 .
①若函数f(x)=[x)-x,x∈R,则值域为(0,1];
②若x,y∈{
| 1 |
| 2 |
| 7 |
| 3 |
| 1 |
| 3 |
③若x∈(1,4),则方程若[x)-x=
| 1 |
| 2 |
④如果数列{an}是等比数列,n∈N*,那么数列{[an)}一定不是等比数列.
其中正确的是
考点:命题的真假判断与应用
专题:新定义,等差数列与等比数列,概率与统计
分析:利用求函数值域的方法,我们分x为整数时和x不为整数时两种情况讨论,易判断①的真假,求出[x)•[y)=3的概率我们易判断②的对错;根据函数零点的求法我们易判断③的正误,利用举反例的方法我们易判断④的对错,进而得到答案.
解答:
解:①当x为整数时,f(x)=[x)-x=(x+1)-x=1,当x不为整数时,f(x)=[x)-x∈(0,1),
故f(x)=[x)-x,值域是(0,1],故①为真命题;
②若x,y∈{
,3,
},则[
)=1,[3)=3,[
)=3,故[x)•[y)=3的概率为
,②不正确;
③当x∈(1,4)时,当且仅当x∈{1.5,2.5,3.5}时,方程[x)-x=
成立,故③x∈(1,4)方程[x)-x=
有3个根为真命题
④如果数列{an}是等比数列,且公比为1,那么数列{[an)}一定是等比数列,故④不正确.
故答案为:①③.
故f(x)=[x)-x,值域是(0,1],故①为真命题;
②若x,y∈{
| 1 |
| 2 |
| 7 |
| 3 |
| 1 |
| 2 |
| 7 |
| 3 |
| 2 |
| 3 |
③当x∈(1,4)时,当且仅当x∈{1.5,2.5,3.5}时,方程[x)-x=
| 1 |
| 2 |
| 1 |
| 2 |
④如果数列{an}是等比数列,且公比为1,那么数列{[an)}一定是等比数列,故④不正确.
故答案为:①③.
点评:本题考查的知识点是命题真假的判断与应用,其中反例法在判断一个全称命题的真假时特别快捷准确,一定要熟练掌握.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
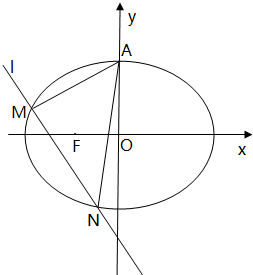 已知椭圆C:
已知椭圆C: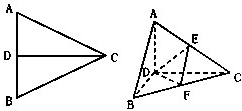 CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示. 如图,设椭圆C:
如图,设椭圆C: