题目内容
对于以下结论:
①若y=f(x)是奇函数,则f(0)=0;
②已知p:事件A、B是对立事件,q:事件A、B是互斥事件,则p是q的必要但不充分条件;
③若
=(1,2),
=(0,-1),则
在
上的投影为-
;
④
<
<
(e为自然数);
⑤函数y=log2
的图象可以由函数y=log2x图象先向左平移2个单位,再向下平移1个单位而得.
其中,正确结论的序号为 .
①若y=f(x)是奇函数,则f(0)=0;
②已知p:事件A、B是对立事件,q:事件A、B是互斥事件,则p是q的必要但不充分条件;
③若
| a |
| b |
| b |
| a |
2
| ||
| 5 |
④
| ln5 |
| 5 |
| ln3 |
| 3 |
| 1 |
| e |
⑤函数y=log2
| x+2 |
| x |
其中,正确结论的序号为
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:据反例说明①错误;根据互斥事件和对立事件的概念判断②;首先求出向量
,
夹角的余弦值,由向量数量积的几何意义求解
在
上的投影判断③;引入辅助函数f(x)=
,由导数判断函数在x>e时为减函数,由此得到命题④的真假;直接利用函数图象的平移求得函数y=log2x平移后的函数解析式,从而判断⑤.
| a |
| b |
| b |
| a |
| lnx |
| x |
解答:
解:对于①,函数f(x)=
是奇函数,但f(0)不存在,∴命题①错误;
对于②,事件A、B是对立事件,则A、B一定是互斥事件,反之,A、B是互斥事件,但A、B不一定是对立事件,∴p是q的充分但不必要条件,命题②错误;
对于③,∵
=(1,2),
=(0,-1),
∴cos<
,
>=
=
=-
.
则
在
上的投影为|
|cos<
,
>=1×(-
)=-
.命题③正确;
对于④,令函数f(x)=
,则f′(x)=
,当x≥e时,f′(x)≤0,
∴函数f(x)=
为减函数,命题④正确;
对于⑤,函数y=log2
=log2(1+
).而函数y=log2x图象向左平移2个单位,再向下平移1个单位得到的函数解析式为y=log2(x+2)-1,∴命题⑤错误.
∴正确结论的序号是③④.
故答案为:③④.
| 1 |
| x |
对于②,事件A、B是对立事件,则A、B一定是互斥事件,反之,A、B是互斥事件,但A、B不一定是对立事件,∴p是q的充分但不必要条件,命题②错误;
对于③,∵
| a |
| b |
∴cos<
| a |
| b |
| ||||
|
|
| 1×0+2×(-1) | ||
|
2
| ||
| 5 |
则
| b |
| a |
| b |
| a |
| b |
2
| ||
| 5 |
2
| ||
| 5 |
对于④,令函数f(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
∴函数f(x)=
| lnx |
| x |
对于⑤,函数y=log2
| x+2 |
| x |
| 2 |
| x |
∴正确结论的序号是③④.
故答案为:③④.
点评:本题考查命题的真假判断与应用,综合考查了函数的性质、图象平移、及单调性的判断,考查了向量数量积的几何意义,考查了互斥事件与对立事件的关系,是中档题.

练习册系列答案
相关题目
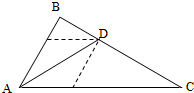 如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且
如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且| AD |
| 1 |
| 4 |
| AC |
| AB |
A、2
| ||
B、3
| ||
C、4
| ||
D、5
|
设p:“a>3”q:“f(x)=x3-ax2+1在(0,2)上有唯一零点”,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: