题目内容
已知函数f（x）=|2x+4|+|x-3|-9．
（1）画出函数y=f（x）的图象；
（2）若当x∈[-4，3]时不等式f（x）＜2a+1恒成立．
（1）画出函数y=f（x）的图象；
（2）若当x∈[-4，3]时不等式f（x）＜2a+1恒成立．
考点：绝对值不等式的解法,函数图象的作法
专题：不等式的解法及应用
分析：（1）先化简函数的解析式，即可画出函数的图象．
（2）由题意可得f（x）max＜2a+1，数形结合求得f（x）max=2，从而求得a的范围．
（2）由题意可得f（x）max＜2a+1，数形结合求得f（x）max=2，从而求得a的范围．
解答：
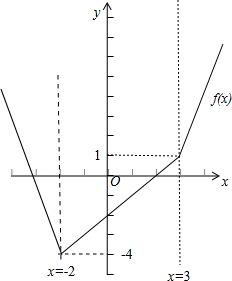解：（1）函数f（x）=|2x+4|+|x-3|-9=
，
如图所示：
（2）当x∈[-4，3]时不等式f（x）＜2a+1恒成立，可得f（x）max＜2a+1．
当x=-4时，f（x）=2；当x=3时，f（x）=1；
再结合图象可可得f（x）max＜2a+1，求得a＞
．
解：（1）函数f（x）=|2x+4|+|x-3|-9=
|
如图所示：
（2）当x∈[-4，3]时不等式f（x）＜2a+1恒成立，可得f（x）max＜2a+1．
当x=-4时，f（x）=2；当x=3时，f（x）=1；
再结合图象可可得f（x）max＜2a+1，求得a＞
| 1 |
| 2 |
点评：本题主要考查带有绝对值的函数，函数的恒成立问题，体现了转化、数形结合的数学思想，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
双曲线
-
=1（0＜m＜3）的焦距为（ ）
| x2 |
| 36-m2 |
| y2 |
| m2 |
| A、6 | ||
| B、12 | ||
| C、36 | ||
D、2
|
下列结论中正确的是（ ）
| A、若两个变量的线性相关性越强，则相关系数的绝对值越接近于0 |
| B、在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0），若ξ位于区域（0，1）的概率为0.4，则ξ位于区域（1，+∞）内的概率为0.6 |
| C、从匀速传递的产品生产流水线上，质检员每4'分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样 |
| D、利用随机变量Χ2来判断“两个独立事件X，Y的关系”时，算出的Χ2值越大，判断“X与Y有关”的把握就越大 |
函数f（x）、g（x）的图象在区间[a，b]上连续不断，且f′（x）•g（x）＞f（x）•g′（x），g（x）＞0，则对任意的x∈（a，b）都有（ ）
| A、f（x）•g（x）＞f（a）•g（b） |
| B、f（x）•g（a）＞f（a）•g（x） |
| C、f（x）•g（x）＞f（b）•g（b） |
| D、f（x）•g（b）＞f（b）•g（x） |
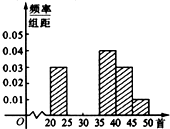某校开展校园文化活动，其中一项是背诵古诗100首，在该项进行一段时间后，随机抽取40人，统计调查了他们会背古诗的首数，得到的数据如下：