题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，已知3cos（B-C）=1+6cosBcosC．
（1）求cosA；
（2）若a=3，△ABC的面积为2
，求b+c的值．
（1）求cosA；
（2）若a=3，△ABC的面积为2
| 2 |
考点：余弦定理
专题：解三角形
分析：（1）已知等式利用两角和与差的余弦函数公式化简，整理后利用两角和与差的余弦函数公式及诱导公式化简，求出cosA的值即可；
（2）由cosA的值求出sinA的值，利用三角形的面积公式表示出三角形ABC面积，把sinA，已知面积代入求出bc的值，利用余弦定理列出关系式，把a与cosA的值代入求出b2+c2的值，利用完全平方公式求出（b+c）2的值，开方即可求出b+c的值．
（2）由cosA的值求出sinA的值，利用三角形的面积公式表示出三角形ABC面积，把sinA，已知面积代入求出bc的值，利用余弦定理列出关系式，把a与cosA的值代入求出b2+c2的值，利用完全平方公式求出（b+c）2的值，开方即可求出b+c的值．
解答：
解：（1）由3cos（B-C）=1+6cosBcosC，
整理得：3cosBcosC-3sinBsinC=-1，
即3cos（B+C）=-1，
∴cosA=-cos（B+C）=
；
（2）∵A为三角形内角，∴sinA=
=
，
∵S△ABC=
bcsinA=2
，
∴bc=6①，
由余弦定理得：a2=b2+c2-2bccosA，即b2+c2=13②，
联立①②，得（b+c）2=b2+c2+2bc=13+12=25，
则b+c=5．
整理得：3cosBcosC-3sinBsinC=-1，
即3cos（B+C）=-1，
∴cosA=-cos（B+C）=
| 1 |
| 3 |
（2）∵A为三角形内角，∴sinA=
| 1-cos2A |
2
| ||
| 3 |
∵S△ABC=
| 1 |
| 2 |
| 2 |
∴bc=6①，
由余弦定理得：a2=b2+c2-2bccosA，即b2+c2=13②，
联立①②，得（b+c）2=b2+c2+2bc=13+12=25，
则b+c=5．
点评：此题考查了余弦定理，三角形面积公式，两角和与差的余弦函数公式，以及诱导公式的作用，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
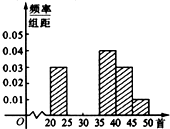某校开展校园文化活动，其中一项是背诵古诗100首，在该项进行一段时间后，随机抽取40人，统计调查了他们会背古诗的首数，得到的数据如下：
如图是某正五棱台灯罩的俯视图，在A，B，C，D，E五个侧面上装裱3种不同的透明中国山水画，相邻区域的中国山水画不同，则不同的装裱方案数是