题目内容
函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，（1）求函数的解析式；
（2）将（1）中的函数图象如图变化才能得到函数y=sinx的图象．
考点：函数y=Asin（ωx+φ）的图象变换,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．
（2）由条件根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
（2）由条件根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答：
解：（1）由函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一部分可得A=3
，
T=
=10-2=8，∴ω=
．
再根据五点法作图可得
×2+φ=
，∴φ=
，故函数的解析式为y=3
sin（
x+
）．
（2）把y=3
sin（
x+
）向右平移2个单位，可得y=3
sin[
（x-2）+
]=3
sin
x的图象；
再把所得图象的横坐标变为原来的
倍，纵坐标不变，可得y=3
sinx的图象；
再把所得图象的纵坐标变为原来的
倍，横坐标不变，可得y=sinx的图象．
| 2 |
| 1 |
| 2 |
| π |
| ω |
| π |
| 8 |
再根据五点法作图可得
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 8 |
| π |
| 4 |
（2）把y=3
| 2 |
| π |
| 8 |
| π |
| 4 |
| 2 |
| π |
| 8 |
| π |
| 4 |
| 2 |
| π |
| 8 |
再把所得图象的横坐标变为原来的
| 8 |
| π |
| 2 |
再把所得图象的纵坐标变为原来的
| 1 | ||
3
|
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
函数f（x）、g（x）的图象在区间[a，b]上连续不断，且f′（x）•g（x）＞f（x）•g′（x），g（x）＞0，则对任意的x∈（a，b）都有（ ）
| A、f（x）•g（x）＞f（a）•g（b） |
| B、f（x）•g（a）＞f（a）•g（x） |
| C、f（x）•g（x）＞f（b）•g（b） |
| D、f（x）•g（b）＞f（b）•g（x） |
若已知α∈（-
，0），且sin（π-α）=log8
，则cos（2π-α）的值等于（ ）
| π |
| 2 |
| 1 |
| 4 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、
|
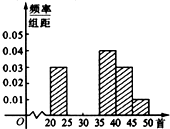某校开展校园文化活动，其中一项是背诵古诗100首，在该项进行一段时间后，随机抽取40人，统计调查了他们会背古诗的首数，得到的数据如下：