题目内容
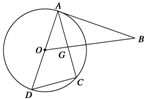如图，已知AD为⊙O的直径，直线BA与⊙O相切于点A，直线OB与弦AC垂直并相交于点G．求证：BA•DC=GC•AD．考点：与圆有关的比例线段
专题：推理和证明
分析：因为AC⊥OB，所以∠AGB=90°，又AD是圆O的直径，所以∠DCA=90°，因为∠BAG=∠ADC，所以Rt△AGB∽Rt△DCA所以
=
，由此能够证明BA•DC=GC•AD．
| BA |
| AD |
| AG |
| DC |
解答：
证明：因为AC⊥OB，所以∠AGB=90°
又AD是圆O的直径，所以∠DCA=90°
又因为∠BAG=∠ADC（弦切角等于同弧所对圆周角）
所以Rt△AGB∽Rt△DCA，
所以
=
，
又因为OG⊥AC，所以GC=AG
所以
=
，故BA•DC=GC•AD．
又AD是圆O的直径，所以∠DCA=90°
又因为∠BAG=∠ADC（弦切角等于同弧所对圆周角）
所以Rt△AGB∽Rt△DCA，
所以
| BA |
| AD |
| AG |
| DC |
又因为OG⊥AC，所以GC=AG
所以
| BA |
| AD |
| GC |
| DC |
点评：本小题主要考查与圆有关的比例线段、三角形相似、弦切角定理、切割线定理等基础知识，考查运算求解能力、化归与转化思想．属于中档题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
为了解某校高三毕业班准备报考飞行员学生的体重情况（体重都以整数计），将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第3小组的频数为6；
某四棱锥的三视图如图所示，该四棱锥的表面积为（ ）
| A、17 | ||
| B、22 | ||
C、14+2
| ||
D、22+2
|
