题目内容

等差数列{an}中，a100=120，a90=100，则公差d等于（　　）
A、2B、20C、100D、不确定
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：直接利用等差数列的通项公式得答案．
解答： 解：在等差数列{an}中，由a100=120，a90=100，得
d=
a100-a90
100-90
=
120-100
10
=2．
故选：A．
点评：本题考查了等差数列的通项公式an=am+（n-m）d，是基础题．
练习册系列答案
相关题目
如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（　　）
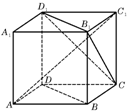
A、BD∥平面CB1D1
B、AC1⊥BD
C、AC1⊥平面CB1D1
D、异面直线AC1与CB所成的角为60°
已知任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有对称中心M（x0，f（x0）），记函数f（x） 的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则f（
1
2014
）+f（
2
2014
）+f（
3
2014
）+…+f（
4017
2014
）=（　　）
A、4027B、-4027
C、8034D、-8034
设f（x）=lnx，g（x）=f（x）+f′（x）．
（1）求g（x）的单调区间和最小值；
（2）讨论g（x）与g（
1
x
）的大小关系．
设集合A={x|0≤x≤2}，B={y|1≤y≤2}，在下图中能表示从集合A到集合B的映射的是（　　）
A、
B、
C、
D、
若cosα-sinα=
1
4
，则sin2α=
 
．
设等差数列{an}的前n项和为Sn，若a2、a4是方程x2-x-1=0的两个实数根，则S5的值为（　　）
A、
5
2
B、5
C、-
5
2
D、-5
若命题“?x∈R，有x2-mx-m＜0”是假命题，则实数m的取值范围是
 
．
已知△ABC中，b=
2
，c=2，sinC+cosC=
2
，则角B=（　　）
A、30°B、45°
C、90°D、150°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网