题目内容
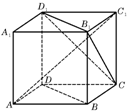
如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（ ）
| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AC1与CB所成的角为60° |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：借助于正方体图形，利用空间中线线、线面、面面间的位置关系判定A、B、C、D选项正确与否，从而确定答案．
解答：
解：∵BD∥B1D1，BD不包含于平面CB1D1，B1D1?平面CB1D1，
∴BD∥平面CB1D1，故A正确；
∵BD⊥CC1，BD⊥AC，CC1∩AC=C，∴BD⊥平面ACC1，
又AC1?平面ACC1，∴AC1⊥BD，故B正确；
∵由三垂线定理知AC1⊥B1D1，AC1⊥B1C，
∴AC1⊥平面CB1D1，故C正确；
由CB∥C1B1，得∠AC1B1，其正切值为
，故D错误．
故选：D．
∴BD∥平面CB1D1，故A正确；
∵BD⊥CC1，BD⊥AC，CC1∩AC=C，∴BD⊥平面ACC1，
又AC1?平面ACC1，∴AC1⊥BD，故B正确；
∵由三垂线定理知AC1⊥B1D1，AC1⊥B1C，
∴AC1⊥平面CB1D1，故C正确；
由CB∥C1B1，得∠AC1B1，其正切值为
| 2 |
故选：D．
点评：本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
下列命题中，否命题为假命题的是（ ）
| A、若同位角相等，则两直线平行 |
| B、若x，y全为0，则x=0且y=0 |
| C、若方程x2+2x+m=0有实根，则m≥0 |
| D、若x2-3x+2＞0，则x2-3x＞0 |
下列集合中表示同一集合的是（ ）
| A、M={（3，2）}，N={（2，3）} |
| B、M={（x，y）|x+y=1}，N={y|x+y=1} |
| C、M={4，5}，N={5，4} |
| D、M={1，2}，N={（1，2）} |
已知A，B，C点在球O的球面上，∠BAC=90°，AB=AC=2．球心O到平面ABC的距离为1，则球O的表面积为（ ）
| A、12π | B、16π |
| C、36π | D、20π |
等差数列{an}中，a100=120，a90=100，则公差d等于（ ）
| A、2 | B、20 | C、100 | D、不确定 |