题目内容
4．已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A． | $\frac{27}{2}$ | B． | 27 | C． | $27\sqrt{2}$ | D． | $27\sqrt{3}$ |
分析 作出棱锥直观图，则每个面都是直角三角形，代入数据计算即可．
解答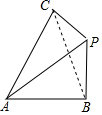 
解：作出几何体的直观图如图所示：
其中PB⊥平面ABC，AB⊥AC，
由三视图可知AB=3，PB=AC=3$\sqrt{3}$，
∴BC=PA=6，
∴S△ABC=$\frac{1}{2}×3×3\sqrt{3}$=$\frac{9\sqrt{3}}{2}$，S△PAB=$\frac{1}{2}×3×3\sqrt{3}$=$\frac{9\sqrt{3}}{2}$，
S△PAC=$\frac{1}{2}×3\sqrt{3}×6$=9$\sqrt{3}$，S△PBC=$\frac{1}{2}×6×3\sqrt{3}$=9$\sqrt{3}$，
∴S表面积=$\frac{9\sqrt{3}}{2}$+$\frac{9\sqrt{3}}{2}$+9$\sqrt{3}$+9$\sqrt{3}$=27$\sqrt{3}$．
故选：D．
点评 本题考查了棱锥的三视图与体积计算，属于中档题．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
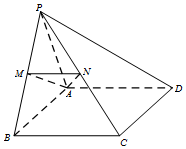在四棱锥P-ABCD中，△PAB为正三角形，四边形ABCD为矩形，平面PAB⊥平面ABCD，AB=2AD，M、N分别为PB、PC的中点．
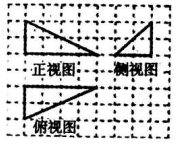如图，网格纸上的小正方形边长为1，粗线画出的是某几何体的三视图，则该几何体外接球的体积为$8\sqrt{6}π$．