题目内容
16.微信是腾讯公司推出的一款手机通讯软件,它支持发送语音、视频、图片和文字等,一推出便风靡全国,甚至涌现出一批在微信朋友圈销售商品的人(被称为微商).经调查,年龄在40岁以下(不包括40岁)的微信用户每天使用微信的时间不低于8小时的概率为$\frac{3}{5}$,年龄在40岁以上(包括40岁)的微信用户每天使用微信的时间不低于8小时的概率为p,将每天使用微信的时间不低于8小时的微信用户称为“微信狂”,若甲(21)岁、乙(36岁)、丙(48岁)三人中有且仅有一人是“微信狂”的概率为$\frac{28}{75}$(1)求甲、乙、丙三人中至少有两人是“微信狂”的概率;
(2)记甲、乙、丙三人中是“微信狂”的人数为X,求随机变量X的分布列和数学期望.
分析 (1)由已知得$\frac{3}{5}×\frac{2}{5}(1-p)+\frac{2}{5}×\frac{3}{5}×(1-p)$+$\frac{2}{5}×\frac{2}{5}p$=$\frac{28}{75}$,求出p=$\frac{1}{3}$.由此能求出甲、乙、丙三人中至少有两人是“微信狂”的概率.
(2)记甲、乙、丙三人中是“微信狂”的人数为X,则X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望EX.
解答 解:(1)∵年龄在40岁以下(不包括40岁)的微信用户每天使用微信的时间不低于8小时的概率为$\frac{3}{5}$,
年龄在40岁以上(包括40岁)的微信用户每天使用微信的时间不低于8小时的概率为p,
将每天使用微信的时间不低于8小时的微信用户称为“微信狂”,
甲(21)岁、乙(36岁)、丙(48岁)三人中有且仅有一人是“微信狂”的概率为$\frac{28}{75}$,
∴$\frac{3}{5}×\frac{2}{5}(1-p)+\frac{2}{5}×\frac{3}{5}×(1-p)$+$\frac{2}{5}×\frac{2}{5}p$=$\frac{28}{75}$,
解得p=$\frac{1}{3}$.
∴甲、乙、丙三人中至少有两人是“微信狂”的概率:
p1=$\frac{3}{5}×\frac{3}{5}×\frac{2}{3}$+$\frac{2}{5}×\frac{3}{5}×\frac{1}{3}$+$\frac{3}{5}×\frac{2}{5}×\frac{1}{3}$+$\frac{3}{5}×\frac{3}{5}×\frac{1}{3}$=$\frac{13}{25}$.
(2)记甲、乙、丙三人中是“微信狂”的人数为X,则X的可能取值为0,1,2,3,
P(X=0)=$\frac{2}{5}×\frac{2}{5}×\frac{2}{3}$=$\frac{8}{75}$,
P(X=1)=$\frac{3}{5}×\frac{2}{5}×\frac{2}{3}$+$\frac{2}{5}×\frac{3}{5}×\frac{2}{3}$+$\frac{2}{5}×\frac{2}{5}×\frac{1}{3}$=$\frac{28}{75}$,
P(X=2)=$\frac{3}{5}×\frac{3}{5}×\frac{2}{3}$+$\frac{2}{5}×\frac{3}{5}×\frac{1}{3}$+$\frac{3}{5}×\frac{2}{5}×\frac{1}{3}$=$\frac{30}{75}$,
P(X=3)=$\frac{3}{5}×\frac{3}{5}×\frac{1}{3}$=$\frac{9}{75}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{75}$ | $\frac{28}{75}$ | $\frac{30}{75}$ | $\frac{9}{75}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件乘法公式的合理运用.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案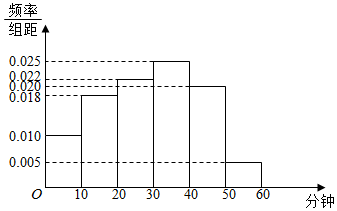 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |