题目内容
8.在△ABC中,A为锐角,|AB|=|AC|+6,|AB|•|AC|=64,且S△ABC=16$\sqrt{3}$,求以B,C为焦点,且过点A的双曲线的方程.分析 利用三角形的面积公式,求出sinA=$\frac{\sqrt{3}}{2}$,可得cosA=$\frac{1}{2}$,利用余弦定理求出|BC|,再建立坐标系,即可求以B,C为焦点,且过点A的双曲线的方程.
解答 解:在△ABC中,∵|AB|•|AC|=64,且S△ABC=16$\sqrt{3}$,
∴$\frac{1}{2}×64×sinA$=16$\sqrt{3}$,
∴sinA=$\frac{\sqrt{3}}{2}$,
∵A为锐角,
∴cosA=$\frac{1}{2}$,
设|AC|=x,|AB|=x+6,∴|BC|=$\sqrt{{x}^{2}+(x+6)^{2}-2x•(x+6)•\frac{1}{2}}$=$\sqrt{x(x+6)+36}$=10,
∴以BC所在直线为x轴,BC的垂直平分线为y轴建立坐标系,可得a=3,c=5,
∴b=4.
∴双曲线的方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1.
点评 本题考查双曲线的定义与方程,考查正弦、余弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.已知x>0,y>0,lg2x+lg8y=lg2,则$\frac{1}{x}+\frac{2}{y}$的最小值是( )
| A. | $7+2\sqrt{6}$ | B. | $4+\sqrt{3}$ | C. | $7+\sqrt{6}$ | D. | $4+2\sqrt{3}$ |
19.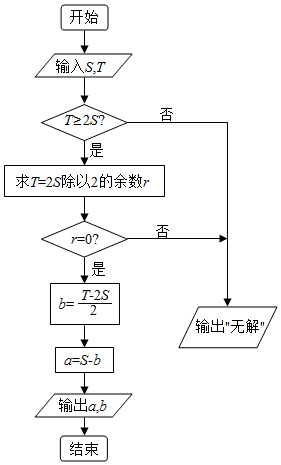 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )| A. | S=40,T=120 | B. | S=40,T=126 | C. | S=42,T=126 | D. | S=42,T=130 |
13.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
17.已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
3.给出以下四个函数的大致图象:则函数f(x)=xlnx,g(x)=$\frac{lnx}{x}$,h(x)=xex,t(x)=$\frac{e^x}{x}$对应的图象序号顺序正确的是( )


| A. | ②④③① | B. | ④②③① | C. | ③①②④ | D. | ④①②③ |