题目内容
5.设f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,已知f(α)=$\frac{5}{6}$,且α∈(0,$\frac{π}{6}$),求sin2α.分析 利用已知条件求出2α的正弦函数与余弦函数方程,利用同角三角函数基本关系式以及两角和与差的三角函数求解即可.
解答 解:f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,f(α)=$\frac{5}{6}$,
可得sin(2α+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{5}{6}$.sin(2α+$\frac{π}{6}$)=$\frac{1}{3}$,
α∈(0,$\frac{π}{6}$),可得2α+$\frac{π}{6}$∈(0,$\frac{π}{2}$).
cos(2α+$\frac{π}{6}$)=$\sqrt{1-si{n}^{2}(2α+\frac{π}{6})}$=$\frac{2\sqrt{2}}{3}$.
sin2α=sin(2α+$\frac{π}{6}$-$\frac{π}{6}$)=sin(2α+$\frac{π}{6}$)cos$\frac{π}{6}$-cos(2α+$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{1}{3}×\frac{\sqrt{3}}{2}$-$\frac{2\sqrt{2}}{3}×\frac{1}{2}$=$\frac{\sqrt{3}-2\sqrt{2}}{6}$.
点评 本题重点考查了三角恒等变换公式、辅助角公式、二倍角公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
10.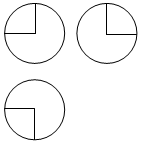 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
17.已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
14.从甲、乙等5名学生中随机选出2人,则甲被选中的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{8}{25}$ | D. | $\frac{9}{25}$ |
 如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.
如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.