题目内容
1.若x、y满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$,若z=x+2y的最大值是6,则z的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 本题考查的知识点是简单的线性规划,我们可以先画出足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域,再根据目标函数z=x+2y的最大值是6,求出点的横坐标即可.
解答 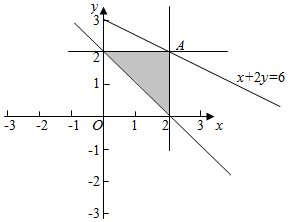 解:满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域如下图:
解:满足约束条件$\left\{\begin{array}{l}x≤a\\ y≤2\\ x+y≥2\end{array}\right.$的平面区域如下图:
∵目标函数z=x+2y的最大值是6,
可得$\left\{\begin{array}{l}{x+2y=6}\\{y=2}\end{array}\right.$,可得A(2,2).
∴当x=2,y=2时,Z取最大值6,
A(2,2)在直线x=a上,可得a=2,
故选:A.
点评 用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
9.如图中的三个直角三角形是一个体积为35cm3的几何体的三视图,则侧视图中的h( )


| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
6.在△ABC中,D为BC的中点,O在AD上且AO=$\frac{1}{4}$AD,AB=2,AC=6,则$\overrightarrow{BC}$•$\overrightarrow{AO}$等于4.
13.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
10.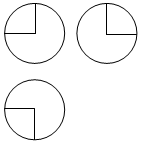 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
16.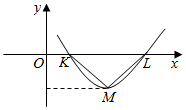 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |