题目内容
16.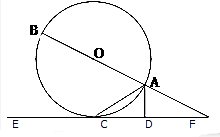 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.(Ⅰ)求证:∠BAC=∠DAC;
(Ⅱ)若OB=2,AD=1,求证:$\frac{BC}{BF}$=$\frac{AF}{BC}$.
分析 (Ⅰ)连接BC,证明∠ACD=∠B,即可证明∠BAC=∠DAC;
(Ⅱ)若OB=2,AD=1,证明AC=2AD,因为AD⊥CE,所以∠ACD=30°.故BC=CF,因为CF与圆O相切,由切割线定理得CF2=AF•BF,即可证明:$\frac{BC}{BF}$=$\frac{AF}{BC}$.
解答 证明: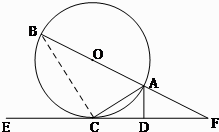 (Ⅰ)连接BC,
(Ⅰ)连接BC,
因为AB是圆O的直径,
所以∠ACB=90°,所以∠B+∠BAC=90°,
因为AD⊥CE,所以∠ACD=∠DAC=90°,
因为AC是弦,且直线CE和圆O切于点C,
所以∠ACD=∠B,
所以∠DAC=∠BAC.…(5分)
(Ⅱ)由(Ⅰ)知△ABC∽△ACD,所以$\frac{AC}{BA}$=$\frac{AD}{AC}$,
由此得AC2=AB•AD,
因为OB=2,AD=1,所以AB=4,求AC2=AB•AD=4×1=4,所以AC=2.
又AD=1,故AC=2AD,
因为AD⊥CE,所以∠ACD=30°.
故BC=CF,因为CF与圆O相切,由切割线定理得CF2=AF•BF,
所以BC2=AF•BF,
即$\frac{BC}{BF}$=$\frac{AF}{BC}$. …(10分)
点评 本题考查圆的切线的性质,考查切割线定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
4.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{lg(x+1),x>0}\end{array}\right.$,则f(f(-3))=( )
| A. | -1 | B. | 0 | C. | 1 | D. | lg2 |
8.在递减数列{an}中,an=-2n2+λn,求实数λ的取值范围是( )
| A. | (-∞,2) | B. | (-∞,3) | C. | (-∞,4) | D. | (-∞,6) |
18.已知点A(2,3)、B (-5,2),若直线l过点P (-1,6),且与线段AB相交,则直线l斜率的取值范围是( )
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
 在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证:
在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证: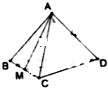 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②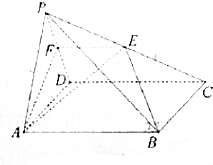 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.