题目内容
18.已知点A(2,3)、B (-5,2),若直线l过点P (-1,6),且与线段AB相交,则直线l斜率的取值范围是( )| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
分析 利用斜率计算公式及其意义即可得出.
解答 解:kPA=$\frac{6-3}{-1-2}$=-1,kPB=$\frac{6-2}{-1-(-5)}$=1,
∵直线l过点P (-1,6),且与线段AB相交,
则直线l斜率的取值范围是(-∞,-1]∪[1,+∞).
故选:B.
点评 本题考查了斜率计算公式及其意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.由曲线y2=2x和直线y=x-4所围成的图形的面积( )
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
10.已知A,B为抛物线y2=2px(p>0)上的两动点,F为其焦点,且满足∠AFB=60°,过弦AB的中点M作抛物线准线的垂线,垂足为N,|MN|=λ|AB|,则λ的最大值为( )
| A. | 1 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
8.双曲线E与椭圆C:$\frac{{x}^{2}}{9}$$+\frac{{y}^{2}}{3}$=1有相同焦点,且以E的一个焦点为圆心与双曲线的渐近线相切的圆的面积为π,则E的离心率为( )
| A. | e=$\sqrt{2}$ | B. | e=$\frac{\sqrt{6}}{2}$ | C. | e=$\frac{\sqrt{30}}{5}$ | D. | e=$\sqrt{3}$ |
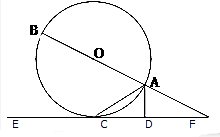 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.