题目内容
8.在递减数列{an}中,an=-2n2+λn,求实数λ的取值范围是( )| A. | (-∞,2) | B. | (-∞,3) | C. | (-∞,4) | D. | (-∞,6) |
分析 由数列{an}是递减数列,可得an+1<an,化简利用数列的单调性即可得出.
解答 解:∵数列{an}是递减数列,∴an+1<an,
∴-2(n+1)2+λ(n+1)<-2n2+λn,
化为:λ<4n+2,
∵数列{4n+2}为单调递增数列,
∴λ<6,
∴实数λ的取值范围是(-∞,6).
故选:D.
点评 本题考查了数列的递推关系、通项公式、单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.函数y=x-sinx在[${\frac{π}{2}$,$\frac{3π}{2}}$]上的最大值是( )
| A. | $\frac{π}{2}$-1 | B. | $\frac{3π}{2}$+1 | C. | $\frac{π}{2}$-$\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3π}{2}$ |
17.由曲线y2=2x和直线y=x-4所围成的图形的面积( )
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
10.已知A,B为抛物线y2=2px(p>0)上的两动点,F为其焦点,且满足∠AFB=60°,过弦AB的中点M作抛物线准线的垂线,垂足为N,|MN|=λ|AB|,则λ的最大值为( )
| A. | 1 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
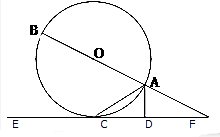 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F. 如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.
如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.