题目内容
6．函数y=log0.2（x2-6x+5）的递增区间是（-∞，1）．分析 求函数的定义域，利用换元法结合复合函数单调性之间的关系进行求解即可．
解答 解：由x2-6x+5＞0得x＞5或x＜1，
设t=x2-6x+5，则当x＞5时，函数t=x2-6x+5为增函数，
当x＜1时，函数t=x2-6x+5为减函数，
而y=log0.2t为减函数，
∴要求函数y=log0.2（x2-6x+5）的递增区间，即求函数t=x2-6x+5的单调递减区间，
∵t=x2-6x+5的单调递减区间是（-∞，1），
故函数y=log0.2（x2-6x+5）的递增区间是（-∞，1），
故答案为：（-∞，1）．
点评 本题主要考查复合函数单调区间的求解，求函数的定义域，利用换元法结合复合函数单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
16．存在函数f（x）满足：对于任意x∈R都有（ ）
| A． | f（sin2x）=sinx | B． | f（x2+2x）=|x+1| | C． | f（sin2x）=x2+x | D． | f（x2+1）=|x+1| |
17．设锐角△ABC的三个内角A，B，C所对的边分别为a，b，c，且b=3，c=1，△ABC的面积为$\sqrt{2}$，则a的值为（ ）
| A． | 2$\sqrt{2}$或2$\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 2$\sqrt{6}$ |
14．在△ABC中，已知A=30°，B=45°，a=1，则b=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
1．设命题p：函数y=sin2x的最小正周期为$\frac{π}{2}$，命题q：函数y=cosx的图象关于直线x=$\frac{π}{2}$对称，则下列判断正确的是（ ）
| A． | p为真 | B． | q为真 | C． | p∧q为假 | D． | p∨q为真 |
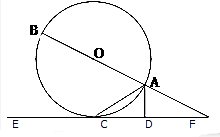如图，AB是圆O的直径，AC是弦，直线EF和圆O相切于点C．AD⊥EF，垂足为D，直线EF交BA的延长线于点F．