题目内容
1.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a4$\overrightarrow{OA}$+a2013$\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),则S2016=1008.分析 由$\overrightarrow{OB}$=a4$\overrightarrow{OA}$+a2013$\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),利用向量共线定理可得:a4+a2013=1.由等差数列{an}的性质可得:a4+a2013=1=a1+a2016.再利用等差数列的前n项和公式即可得出.
解答 解:∵$\overrightarrow{OB}$=a4$\overrightarrow{OA}$+a2013$\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),
∴a4+a2013=1.
由等差数列{an}的性质可得:a4+a2013=1=a1+a2016.
则S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008,
故答案为:1008.
点评 本题考查了向量共线定理、等差数列的性质、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.在平面直角坐标系xOy中,已知曲线C1:$\left\{\begin{array}{l}{x=1-t}\\{y=4-2t}\end{array}\right.$(t为参数)与曲线C2:$\left\{\begin{array}{l}{x=2+rcosθ}\\{y=1+rsinθ}\end{array}\right.$ (θ为参数,r>0)有一个公共点在y轴上,则r=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
6.下列函数中,在[-1,0]上单调递减的是( )
| A. | y=cosx | B. | y=-|x-1| | C. | y=log${\;}_{\frac{1}{2}}}$$\frac{2-x}{2+x}$ | D. | y=ex+e-x |
13.函数y=x-sinx在[${\frac{π}{2}$,$\frac{3π}{2}}$]上的最大值是( )
| A. | $\frac{π}{2}$-1 | B. | $\frac{3π}{2}$+1 | C. | $\frac{π}{2}$-$\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3π}{2}$ |
10.定义在R上的偶函数f(x),对任意x0∈[0,+∞)总存在正实数d,有$\frac{f({x}_{0}+d)-f({x}_{0})}{d}$<0,则( )
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
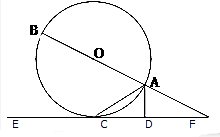 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.