题目内容
4.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{lg(x+1),x>0}\end{array}\right.$,则f(f(-3))=( )| A. | -1 | B. | 0 | C. | 1 | D. | lg2 |
分析 根据函数的解析式求出f(-3)的值,从而求出f(f(-3))的值即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{lg(x+1),x>0}\end{array}\right.$,
∴f(-3)=9,∴f(f(-3))=f(9)=lg10=1,
故选:C.
点评 本题考查了函数求值问题,考查导数的运算,是一道基础题.

练习册系列答案
相关题目
14.在△ABC中,已知A=30°,B=45°,a=1,则b=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.在平面直角坐标系xOy中,已知曲线C1:$\left\{\begin{array}{l}{x=1-t}\\{y=4-2t}\end{array}\right.$(t为参数)与曲线C2:$\left\{\begin{array}{l}{x=2+rcosθ}\\{y=1+rsinθ}\end{array}\right.$ (θ为参数,r>0)有一个公共点在y轴上,则r=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
13.函数y=x-sinx在[${\frac{π}{2}$,$\frac{3π}{2}}$]上的最大值是( )
| A. | $\frac{π}{2}$-1 | B. | $\frac{3π}{2}$+1 | C. | $\frac{π}{2}$-$\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3π}{2}$ |
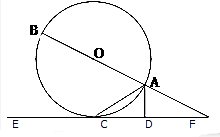 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.