题目内容
11.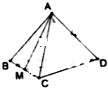 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②①BC⊥平面AMD
②点Q一定在直线DM上
③VC-AMD=4$\sqrt{2}$.
分析 由题意画出图形,利用线面垂直的判定判断①;由面面垂直的判定得到平面ABC⊥平面AMD,再由面面垂直的性质判断②;直接求出VC-AMD判断③.
解答 解:如图,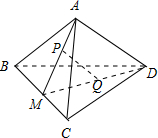
∵四面体A-BCD的所有棱长相等,
∴四面体为正四面体,
又M为BC的中点,
∴AM⊥BC,DM⊥BC,则BC⊥平面AMD,故①正确;
∵BC?平面ABC,
∴平面ABC⊥平面AMD,又平面AMD∩平面ABC=AM,且PQ⊥AM,
由平面与平面垂直的性质可得,PQ?平面AMD,则点Q一定在直线DM上,故②正确;
${S}_{△ABC}=\frac{1}{2}×4×\sqrt{{4}^{2}-{2}^{2}}=4\sqrt{3}$,四棱锥的高h=$\sqrt{{4}^{2}-(\frac{4}{3}\sqrt{3})^{2}}=\frac{4\sqrt{6}}{3}$.
∴VC-AMD=$\frac{1}{2}×\frac{1}{3}×4\sqrt{3}×$$\frac{4\sqrt{6}}{3}$=$\frac{8\sqrt{2}}{3}$,故③错误.
∴正确的命题是①②.
故答案为:①②.
点评 本题考查命题的真假判断与应用,考查棱锥的结构特征,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
1.设命题p:函数y=sin2x的最小正周期为$\frac{π}{2}$,命题q:函数y=cosx的图象关于直线x=$\frac{π}{2}$对称,则下列判断正确的是( )
| A. | p为真 | B. | q为真 | C. | p∧q为假 | D. | p∨q为真 |
2.已知函数f(x)=2x-x-2的一个零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,3) | D. | (3,4) |
 某学校组织学生参加英语测试,成绩的频率分布直方图如图,若低于60分的人数是15人,则不低于80分的学生人数是15.
某学校组织学生参加英语测试,成绩的频率分布直方图如图,若低于60分的人数是15人,则不低于80分的学生人数是15.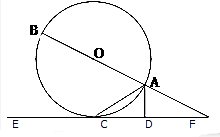 如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F.
如图,AB是圆O的直径,AC是弦,直线EF和圆O相切于点C.AD⊥EF,垂足为D,直线EF交BA的延长线于点F. 如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.
如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.