题目内容
6.将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为( )| A. | 2π | B. | 3π | C. | 4π | D. | 6π |
分析 判断几何体的特征,然后求解即可.
解答 解:由题意知,该几何体为半球,表面积为大圆面积加上半个求面积,$S=π×{1^2}+\frac{1}{2}×4×π×{1^2}=3π$,
故选:B.
点评 本题考查旋转体的几何特征,球的表面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
18.已知f(x)是定义在[-2,2]上的奇函数,当x∈(0,2]时,f(x)=2x-1,函数g(x)=x2-2x+m,如果对于任意x1∈[-2,2],存在x2∈[-2,2],使得g(x2)=f(x1),则实数m的取值范围是( )
| A. | (-∞,-2) | B. | (-5,-2) | C. | [-5,-2] | D. | (-∞,-2] |
15.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-3),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
16.若a>b,则下列选项一定成立的是( )
| A. | a2>b2 | B. | ac>bc | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ac2≥bc2 |
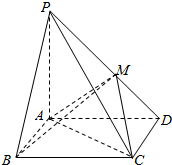 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.