题目内容
12. 在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.
在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.
分析 由$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$=$\overrightarrow{AB}+\overrightarrow{AD}$,可得${\overrightarrow{BD}}^{2}+{\overrightarrow{AC}}^{2}$=$2({\overrightarrow{AD}}^{2}+{\overrightarrow{AB}}^{2})$,即可得出.
解答 解:∵$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$=$\overrightarrow{AB}+\overrightarrow{AD}$,∴${\overrightarrow{BD}}^{2}+{\overrightarrow{AC}}^{2}$=$2({\overrightarrow{AD}}^{2}+{\overrightarrow{AB}}^{2})$,
∴32+${\overrightarrow{AC}}^{2}$=2(22+32),
解得$\overrightarrow{|AC}|$=$\sqrt{17}$.
点评 本题考查了向量的三角形法则、平行四边形法则、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.△ABC中,内角A和B满足关系式cosAcosB>sinA•sinB,那么△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 任意三角形 |
2.已知0<a<b<c,且a,b,c是成等比数列的整数,n为大于1的整数,则logan,logbn,logcn( )
| A. | 成等差数列 | B. | 成等比数列 | ||
| C. | 各项倒数成等差数列 | D. | 以上都不对 |
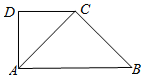 已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.