题目内容

2．已知0＜a＜b＜c，且a，b，c是成等比数列的整数，n为大于1的整数，则logan，logbn，logcn（　　）
A．成等差数列B．成等比数列
C．各项倒数成等差数列D．以上都不对

分析 a，b，c是成等比数列的整数，可得b2=ac．计算$\frac{2}{lo{g}_{b}n}$-$\frac{1}{lo{g}_{a}n}$-$\frac{1}{lo{g}_{c}n}$即可判断出结论．

解答 解：∵a，b，c是成等比数列的整数，∴b2=ac．
∵n为大于1的整数，0＜a＜b＜c，
∴$\frac{2}{lo{g}_{b}n}$-$\frac{1}{lo{g}_{a}n}$-$\frac{1}{lo{g}_{c}n}$
=2lognb-logan-logcn
=$lo{g}_{n}\frac{{b}^{2}}{ac}$=logn1=0，
则logan，logbn，logcn各项倒数成等差数列．
故选：C．

点评 本题考查了等差数列与等比数列的通项公式及其性质、对数的运算性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．在□ABCD中，AD=2，AB=3，对角线BD=3，试用向量的方法求对角线AC的长．
13．已知数列{an}的前n项和Sn=27-33-n，则数列{anan+1an+2}的前3项和等于（　　）
A．216B．224C．$\frac{6056}{27}$D．26
10．化简：${C}_{m}^{7}$-C${\;}_{m+1}^{8}$+C${\;}_{m}^{8}$．
17．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，且|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，则向量2$\overrightarrow{a}$+3$\overrightarrow{b}$在向量2$\overrightarrow{a}$+$\overrightarrow{b}$方向上的投影为（　　）
A．$\frac{19\sqrt{13}}{13}$B．$\frac{6\sqrt{13}}{13}$C．$\frac{5\sqrt{6}}{6}$D．$\frac{8\sqrt{3}}{13}$
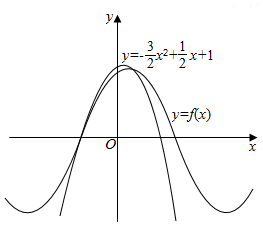7．如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上，则f（x）=sin（$\frac{π}{2}$x+$\frac{π}{3}$）．
14．若sinx-sin（$\frac{3π}{2}$-x）=$\sqrt{2}$，则 tan x+tan（$\frac{3π}{2}$-x）的值是（　　）
A．-2B．-1C．1D．2
11．已知复数z1=2+3i，z2=a+bi（a，b∈R），z3=1-4i在复平面内对应的点分别为A，B，C，O为原点，若$\overrightarrow{OC}$=2$\overrightarrow{OA}$+$\overrightarrow{OB}$，则3a-b=1．
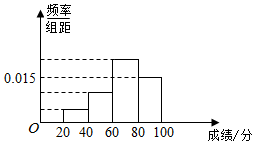2．北京市某校组织学生惨叫英语测试，某班50人的成绩的频率分布直方图如图所示，数据的分组依次为[20，40），[40，60），[60，80），[80，100），已知前3组的人数依次构成等比数列，第2组、第4组、第3组的人数依次构成等差数列，则及格（大于等于60分）的人数是35．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网