题目内容
17.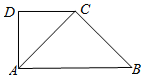 已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
分析 不妨设AD=1,则DC=1,AC=$\sqrt{2}$,BC=$\sqrt{2}$,AB=2,根据三棱锥体积最大时,得到DE⊥平面ABC,根据二面角的定义作出二面角的平面角,进行求解即可.
解答 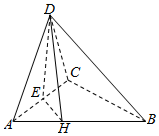 解:AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,
解:AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,
∴不妨设AD=1,则DC=1,AC=$\sqrt{2}$,BC=$\sqrt{2}$,AB=2,
则AD⊥CD,AC⊥BC,
取AC的中点E,则DE⊥AC,
若棱锥D-ABC的体积最大时,
∵底面△ABC的面积是定值,
∴只要三棱锥的高最大即可,
此时满足DE⊥平面ABC,即可.
过E作EH⊥AB,连接DH,
则DH⊥AB,
即∠DHE是二面角D-AB-C的平面角,
则tan∠DHE=$\frac{DE}{EH}$,
∵在等腰直角三角形ADC中,AD=1,∴DE=$\frac{\sqrt{2}}{2}$,AE=$\frac{\sqrt{2}}{2}$,
则等腰直角三角形ACB中,EH=AEsin45°=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{2}$,
则tan∠DHE=$\frac{DE}{EH}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$
点评 本题主要考查二面角的求解,根据三棱锥体积最大值时确定DE⊥平面ABC是解决本题的关键.利用定义法作出二面角的平面角是本题的难点.

练习册系列答案
相关题目
7.设全集U=R,A={x∈N|-1≤x≤10},B={x∈R|x2-x-6=0},则图中阴影部分表示的集合为( )
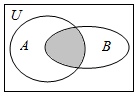

| A. | {3} | B. | {2} | C. | {3,2} | D. | {-2,3} |
2.若O为△ABC内一点,且2$\overrightarrow{OA}$$+7\overrightarrow{OB}$$+6\overrightarrow{OC}$=$\overrightarrow{0}$,三角形ABC的面积是三角形OAB面积的λ倍,则λ=( )
| A. | $\frac{5}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{15}{7}$ | D. | 5 |
6.要得到函数y=3sin2x(x∈R)的图象,只要将函数y=3sin(2x+1)(x∈R)的图象( )
| A. | 向左平移1个位长度,纵坐标不变 | B. | 向右平移1个位长度,纵坐标不变 | ||
| C. | 向左平移$\frac{1}{2}$个位长度,纵坐标不变 | D. | 向右平移$\frac{1}{2}$个位长度,纵坐标不变 |
 在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.
在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.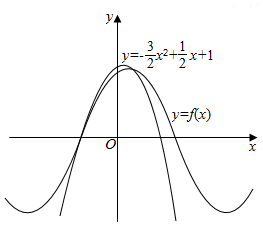 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).