题目内容
2.已知数列{an}满足a1=1,an+1=1+an,(n∈N*),A=-a1a2+a2a3-a3a4+a4a5-…+a2na2n+1,则A=2n(n+1).分析 可判断数列{an}是以1为首项,1为公差的等差数列,从而可得an=n,进而可得-a2n-1a2n+a2na2n+1=4n,从而求和即可.
解答 解:∵a1=1,an+1=1+an,
∴数列{an}是以1为首项,1为公差的等差数列,
∴an=n,
∴-a2n-1a2n+a2na2n+1=a2n(a2n+1-a2n-1)=2n(2n+1-(2n-1))=4n,
∴A=-a1a2+a2a3-a3a4+a4a5-…+a2na2n+1
=(-a1a2+a2a3)+(-a3a4+a4a5)+…+(-a2n-1a2n+a2na2n+1)
=4+8+…+4n=$\frac{4+4n}{2}n$=2n(n+1),
故答案为:2n(n+1).
点评 本题考查了等差数列的性质的判断与应用,同时考查了并项求和法的应用及转化思想的应用.

练习册系列答案
相关题目
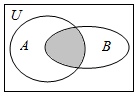
7.设全集U=R,A={x∈N|-1≤x≤10},B={x∈R|x2-x-6=0},则图中阴影部分表示的集合为( )

| A. | {3} | B. | {2} | C. | {3,2} | D. | {-2,3} |
14.已知函数$f(x)=\left\{\begin{array}{l}{x^3}\\ sinx\end{array}\right.$$\begin{array}{l}x≥0\\ x<0\end{array}$,则$f[f(-\frac{3π}{2})]$=( )
| A. | -sin1 | B. | sin1 | C. | -1 | D. | 1 |
11.复数$\frac{1}{{i}^{5}}$的虚部为( )
| A. | 1 | B. | -1 | C. | 0 | D. | -i |
 在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.
在□ABCD中,AD=2,AB=3,对角线BD=3,试用向量的方法求对角线AC的长.