题目内容
已知集合M={x∈R|(x+1)(x-2)>0}和N={x∈R|x2+x<0},则集合M是集合N的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先求出关于集合M,N的不等式,结合集合之间的关系,从而得到答案.
解答:
解:∵M={x|x>2或x<1},N={x|-1<x<1},
∴集合M是集合N的既不充分也不必要条件,
故选:D.
∴集合M是集合N的既不充分也不必要条件,
故选:D.
点评:本题考查了充分必要条件,考查了集合之间的关系,是一道基础题.

练习册系列答案
相关题目
若数列{an}是等差数列,则“a1<a2”是“数列{an}为递增数列”( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分也不必要条件 |
已知向量
,
满足|
|=1,|
|=2,且(
+
)⊥
,则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
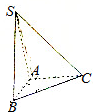 如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC. 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.