题目内容
给出下列四个命题:
①△ABC中,A>B是sinA>sinB成立的充要条件;
②当x>0且x≠1时,有lnx+
≥2;
③已知Sn是等差数列{an}的前n项和,若S7>S5,则S9>S3;
④若函数y=f(x-
)为R上的奇函数,则函数y=f(x)的图象一定关于点F(
,0)成中心对称.
其中所有正确命题的序号为 .
①△ABC中,A>B是sinA>sinB成立的充要条件;
②当x>0且x≠1时,有lnx+
| 1 |
| lnx |
③已知Sn是等差数列{an}的前n项和,若S7>S5,则S9>S3;
④若函数y=f(x-
| 3 |
| 2 |
| 3 |
| 2 |
其中所有正确命题的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用,等差数列与等比数列,解三角形,简易逻辑
分析:由三角形中的大边对大角结合正弦定理判断①;举反例说明②错误;根据等差数列的性质可说明③正确;直接由函数图象的平移说明④错误.
解答:
解:对于①,由A>B,得边a>边b(大角对大边),
根据正弦定理知:
=
,
则sinA>sinB;
由sinA>sinB,根据正弦定理知:
=
,
则边a>边b,根据大边对大角,则有A>B.
∴△ABC中,A>B是sinA>sinB成立的充要条件.命题①正确;
对于②,若0<x<1,则lnx<0,lnx+
≥2不成立.命题②错误;
对于③,等差数列{an}若S7>S5,则2a1+11d>0,则S9-S3=6a1+33d>0,即S9>S3,命题③正确;
对于④,函数y=f(x-
)为R上的奇函数,则其图象关于(0,0)中心对称,
而函数y=f(x)的图象是把y=f(x-
)的图象向左平移
个单位得到的,
∴函数y=f(x)的图象一定关于点F(-
,0)成中心对称.命题④错误.
故答案为:①③
根据正弦定理知:
| a |
| sinA |
| b |
| sinB |
则sinA>sinB;
由sinA>sinB,根据正弦定理知:
| a |
| sinA |
| b |
| sinB |
则边a>边b,根据大边对大角,则有A>B.
∴△ABC中,A>B是sinA>sinB成立的充要条件.命题①正确;
对于②,若0<x<1,则lnx<0,lnx+
| 1 |
| lnx |
对于③,等差数列{an}若S7>S5,则2a1+11d>0,则S9-S3=6a1+33d>0,即S9>S3,命题③正确;
对于④,函数y=f(x-
| 3 |
| 2 |
而函数y=f(x)的图象是把y=f(x-
| 3 |
| 2 |
| 3 |
| 2 |
∴函数y=f(x)的图象一定关于点F(-
| 3 |
| 2 |
故答案为:①③
点评:本题考查了命题的真假判断与应用,考查了充分必要条件的判断方法,考查了函数图象的平移,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若数列{an}是等差数列,则“a1<a2”是“数列{an}为递增数列”( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分也不必要条件 |
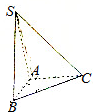 如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥AC. 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.