题目内容
某学校在“11•9”举行老师、学生消防知识比赛，报名的学生和教师的人数之比为6：1，学校决定按分层抽样的方法从报名的师生中抽取35人组队进行比赛，已知教师甲被抽到的概率为
，则报名的学生人数是 ．
| 1 |
| 10 |
考点：分层抽样方法
专题：概率与统计
分析：根据题意，可得教师、学生的抽取人数，又由教师甲被抽到的概率为
，可得每个个体被抽到的概率，进而由等可能事件的概率公式计算可得答案．
| 1 |
| 10 |
解答：
解：根据题意，报名的学生和教师的人数之比为6：1，且共抽取了35人，
则教师抽取了35
=5人，学生抽取了35-5=30人，
教师甲被抽到的概率为
，则每个学生被抽到的概率均为
，
则报名的学生人数是30÷
=300；
故答案为：300；
则教师抽取了35
| 1 |
| 6+1 |
教师甲被抽到的概率为
| 1 |
| 10 |
| 1 |
| 10 |
则报名的学生人数是30÷
| 1 |
| 10 |
故答案为：300；
点评：本题考查分层抽样方法的运用，注意分层抽样中每个个体被抽到的概率都相等，均为
．
| n |
| N |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l，m，平面α，β满足l⊥α，m?β，则“l⊥m”是“α∥β”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
当x＞0时，下列函数中最小值为2的是（ ）
A、y=x+
| ||
| B、y=x2-2x+3 | ||
C、y=
| ||
D、y=lnx+
|
若数列{an}是等差数列，则“a1＜a2”是“数列{an}为递增数列”（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分也不必要条件 |
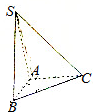如图，在三棱锥S-ABC中，SA⊥底面ABC，AB⊥AC．