题目内容
 如图,ABCD是边长为2的正方形,ED⊥ABCD,ED=1,EF∥BD,且EF=
如图,ABCD是边长为2的正方形,ED⊥ABCD,ED=1,EF∥BD,且EF=| 1 |
| 2 |
(1)求证:BF∥平面ACE;
(2)求证:平面EAC⊥平面BDEF;
(3)求二面角B-AF-C的大小.
考点:平面与平面垂直的判定,直线与平面平行的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(1)记AC与BD的交点为O,则DO=BO=
BD,连接EO,则可证出四边形EFBO是平行四边形,从而BF∥EO,最后结合线面平行的判定定理,可得BF∥平面ACE;
(2)由正方形性质得AC⊥BD,由线面垂直得AC⊥ED,从而得以AC⊥平面BDEF,由此能证明面EAC⊥面BDEF.
(3)证明BO⊥面ACF,过点O作OG⊥AF于点G,连接GB,则∠OGB为二面角B-AF-C的平面角,则可求;
| 1 |
| 2 |
(2)由正方形性质得AC⊥BD,由线面垂直得AC⊥ED,从而得以AC⊥平面BDEF,由此能证明面EAC⊥面BDEF.
(3)证明BO⊥面ACF,过点O作OG⊥AF于点G,连接GB,则∠OGB为二面角B-AF-C的平面角,则可求;
解答:
(1)证明:记AC与BD的交点为O,则DO=BO=
BD,连接EO,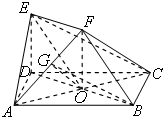
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE.
(2)证明:∵ABCD是边长为2的正方形,
∴AC⊥BD,
∵ED⊥面ABCD,AC?面ABCD,
∴AC⊥ED,
∵BD∩ED=D,∴AC⊥平面BDEF,
又AC?平面EAC,∴平面EAC⊥平面BDEF.
(3)解::∵ABCD为正方形,∴BO⊥AC,
∵EF∥BD且EF=
BD,
∴EFOD为平行四边形,
∴ED∥OF,OF⊥面ABCD,
∴OF⊥BO,
∵AC∩OF=O,
∴BO⊥面ACF,
过点O作OG⊥AF于点G,连接GB,则∠OGB为二面角B-AF-C的平面角.
在Rt△FOA中,可求得OG=
=
,
∵OB=
,
∴tan∠OGB=
,
∴∠OGB=
,
∴二面角B-AF-C的大小为
.
| 1 |
| 2 |

∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE.
(2)证明:∵ABCD是边长为2的正方形,
∴AC⊥BD,
∵ED⊥面ABCD,AC?面ABCD,
∴AC⊥ED,
∵BD∩ED=D,∴AC⊥平面BDEF,
又AC?平面EAC,∴平面EAC⊥平面BDEF.
(3)解::∵ABCD为正方形,∴BO⊥AC,
∵EF∥BD且EF=
| 1 |
| 2 |
∴EFOD为平行四边形,
∴ED∥OF,OF⊥面ABCD,
∴OF⊥BO,
∵AC∩OF=O,
∴BO⊥面ACF,
过点O作OG⊥AF于点G,连接GB,则∠OGB为二面角B-AF-C的平面角.
在Rt△FOA中,可求得OG=
| FO•AO |
| AF |
| ||
| 3 |
∵OB=
| 2 |
∴tan∠OGB=
| 3 |
∴∠OGB=
| π |
| 3 |
∴二面角B-AF-C的大小为
| π |
| 3 |
点评:本题以一个特殊多面体为例,要我们证明线面平行和面面垂直,着重考查了线面平行的判定定理和面面垂直的判定理等知识,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
设
、
都是非零向量,下列四个条件中,一定能使
+
=
成立的是( )
| a |
| b |
| ||
|
|
| ||
|
|
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列命题中的假命题是( )
| A、以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫圆柱 |
| B、以直角三角形的一条边所在的直线为旋转轴,其余两边旋转形成的曲面的旋转体叫圆锥 |
| C、以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的旋转体叫圆锥 |
| D、以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成的曲面围成的旋转体叫圆锥 |