题目内容
设
、
都是非零向量，下列四个条件中，一定能使
+
=
成立的是（ ）
| a |
| b |
| ||
|
|
| ||
|
|
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点：平行向量与共线向量
专题：平面向量及应用
分析：根据向量共线定理，可得若
+
=
成立，则向量
、
共线且方向相反，对照各个选项并结合数乘向量的含义，可得本题答案．
| ||
|
|
| ||
|
|
| 0 |
| a |
| b |
解答：
解：由
+
=
得若
=-
=
，即
=-
•
，则向量
、
共线且方向相反，
因此当向量
、
共线且方向相反时，能使
+
=
成立，
对照各个选项，可得B项中向量
、
的方向相同或相反，
C项中向量向量
、
的方向相同，
D项中向量
、
的方向互相垂直．
只有A项能确定向量
、
共线且方向相反．
故选：A
| ||
|
|
| ||
|
|
| 0 |
| ||
|
|
| ||
|
|
| 0 |
| b |
|
| ||
|
|
| a |
| a |
| b |
因此当向量
| a |
| b |
| ||
|
|
| ||
|
|
| 0 |
对照各个选项，可得B项中向量
| a |
| b |
C项中向量向量
| a |
| b |
D项中向量
| a |
| b |
只有A项能确定向量
| a |
| b |
故选：A
点评：本题考查了数乘向量的含义与向量共线定理等知识，属于基础题．
练习册系列答案
相关题目
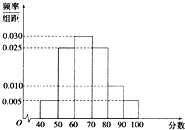某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40、50），[50、60），[60、70），[70、80），[80、90），[90、100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ ）| A、588 | B、420 |
| C、450 | D、120 |
已知向量
=（-2，4），
=（1，-2），则
与
的关系是（ ）
| a |
| b |
| a |
| b |
| A、不共线 | B、相等 | C、同向 | D、反向 |
已知复数z满足：（1+i）•z=2i，则|z|=（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
执行如图所示的程序框图，若输入的x值为
，则输出的y的值为（ ）
| 1 |
| 2 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
用数学归纳法证明
+
+…+
＞
时，由k到k+1，不等式左边的变化是（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 11 |
| 34 |
A、增加
| ||||||
B、增加
| ||||||
C、增加
| ||||||
| D、以上结论都不对 |
在△ABC中，
=
，
=
，且
•
＞0，则△ABC是（ ）
| AB |
| a |
| BC |
| b |
| a |
| b |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、钝角三角形 |
直线
，上对应t=0，t=1，两点间的距离是（ ）
|
| A、1 | ||
B、
| ||
| C、10 | ||
D、2
|
如图，ABCD是边长为2的正方形，ED⊥ABCD，ED=1，EF∥BD，且EF=