题目内容
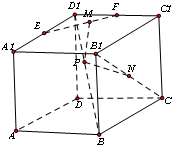
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱A1D1,C1D1的中点,N为线段B1C的中点,若点P,M分别为线段D1B,EF上的动点,则PM+PN的最小值为( )

| A、1 | ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键),最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH,即可得出结论.
解答:
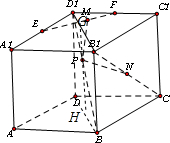 解:首先PM的最小值就是P到EF的距离.
解:首先PM的最小值就是P到EF的距离.
连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键)
最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH.
∵正方体ABCD-A1B1C1D1的棱长为1,
∴GH=
=
.
故选:B.
 解:首先PM的最小值就是P到EF的距离.
解:首先PM的最小值就是P到EF的距离. 连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键)
最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH.
∵正方体ABCD-A1B1C1D1的棱长为1,
∴GH=
1+(
|
3
| ||
| 4 |
故选:B.
点评:本题考查多面体和旋转体表面上的最短距离问题,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0),过双曲线的一个焦点作实轴的垂线交双曲线于A、B两点,若
•
=0(O为坐标原点),则双曲线的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
函数f(a)=(3m-1)a+b-2m,当m∈[0,1]时,0≤f(a)≤1恒成立,则
的最大值是( )
| b2-a2 |
| ab |
A、
| ||
| B、4 | ||
C、
| ||
| D、5 |
函数f(x)=
+3(x>0)的最小值是( )
| x3+x |
| x2 |
| A、5 | |||
B、3
| |||
| C、3 | |||
| D、2 |
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案,在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,则下列哪个奖励模型比较符合该公司的要求( )
| A、y=0.25x | |||
| B、y=log7x+1 | |||
| C、y=1.002x | |||
D、y=
|
已知x,y满足
,则z=2x+y的最小值是( )
|
| A、3 | ||
| B、-3 | ||
C、
| ||
| D、0 |