题目内容
11.三角形ABC中,C=90°,A=30°,过C作射线l交线段AB于点D,则S△ABC>2S△ACD的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 取AB中点D0,得△ACD0的面积等于△ABC的面积的一半,当经过C点的射线CD位于∠ACD0内部时,满足S△ABC>2S△ACD,因此用∠ACD0的度数除以∠ABC的度数,即得本题的概率.
解答 解:取AB中点D0,得△ACD0的面积等于△ABC的面积的一半.
∵Rt△ABC中,∠C=90°,∠A=30°,
∴CD0=BD0=BC=$\frac{1}{2}$AB,可得∠ACD0=30°
当经过C点的射线CD位于∠SCD0内部时,S△ABC>2S△ACD,
∴所求概率为P=$\frac{30}{90}$=$\frac{1}{3}$.
故选:A.
点评 本题给出含有60°的直角三角形,求射线截三角形所得面积小于直角三角形面积一半的概率,着重考查了几何概型及其计算方法的知识,属于基础题.

练习册系列答案
相关题目
1.若关于x的不等式x2+2x-k>0的解集为R,则实数k的取值范围是( )
| A. | {k|k≤-1或k≥1} | B. | {k|-1<k<1} | C. | {k|k<-1} | D. | {k|k≤-1} |
19.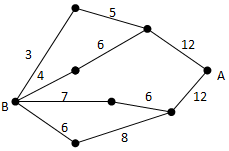 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
16.要排出某班一天中语文、数学、政治、英语、体育、艺术六堂课的课程表,要求数学排在上午(前4节),体育排在下午(后2节),不同排法总数是( )
| A. | 720 | B. | 120 | C. | 144 | D. | 192 |
3.已知集合A={-3,-2,-1,0,1,2,3},B={y|y=2x,x∈R},则A∩(∁RB)=( )
| A. | {0,1,2,3} | B. | {1,2,3} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1} |
20.如图为一个简单组合体的三视图,其中正视图由 一个半圆和一个正方形组成,则该组合体的表面积为( )
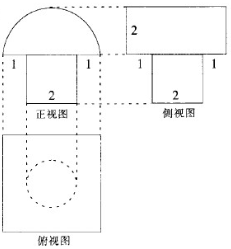

| A. | 20+17π | B. | 20+16π | C. | 16+17π | D. | 16+l6π |



