题目内容
6.设k∈R,则函数f(x)=sin(kx+$\frac{π}{6}$)+k的部分图象不可能是( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 对k取值,结合函数的图象,即可得出结论.
解答 解:k=0,y=$\frac{1}{2}$,故A正确;
k=2,f(x)=sin(2x+$\frac{π}{6}$)+2,图象为B,B正确;
k=-1,f(x)=sin(-x+$\frac{π}{6}$)-1,图象为C,C正确;
k=1,f(x)=sin(x+$\frac{π}{6}$)+1,x∈(0,$\frac{π}{3}$),函数单调递增,D不正确.
故选D.
点评 本题考查函数的图象与性质,考查数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知m为实数,i为虚数单位,若m+(m2-1)i>0,则$\frac{m+i}{1-i}$=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
1.已知AD为△ABC的中线,则$\overrightarrow{AD}$=( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$ | C. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AC}$ | D. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$ |
11.三角形ABC中,C=90°,A=30°,过C作射线l交线段AB于点D,则S△ABC>2S△ACD的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
18.若函数f(x)=x3-12x在区间(k,k+2)上不是单调函数,则实数k的取值范围( )
| A. | k≤-4或-2≤k≤0或k≥2 | B. | -4<k<2 | ||
| C. | -4<k<-2或0<k<2 | D. | 不存在这样的实数k |
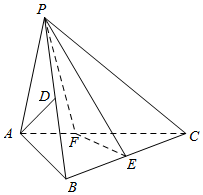 如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.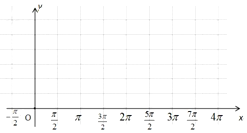 已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$
已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$