题目内容
3.已知集合A={-3,-2,-1,0,1,2,3},B={y|y=2x,x∈R},则A∩(∁RB)=( )| A. | {0,1,2,3} | B. | {1,2,3} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1} |
分析 根据补集的定义求得∁RB,再根据两个集合的交集的定义,求得A∩(∁RB).
解答 解:∵B={y|y=2x,x∈R}=(0,+∞),∴∁RB=(-∞,0],
∵A={-3,-2,-1,0,1,2,3},
∴A∩(∁RB)={-3,-2,-1,0}
故选:C.
点评 本题考查了集合中交集与补集的运算,属于集合运算中的基础题,应当掌握.

练习册系列答案
相关题目
11.三角形ABC中,C=90°,A=30°,过C作射线l交线段AB于点D,则S△ABC>2S△ACD的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
18.若函数f(x)=x3-12x在区间(k,k+2)上不是单调函数,则实数k的取值范围( )
| A. | k≤-4或-2≤k≤0或k≥2 | B. | -4<k<2 | ||
| C. | -4<k<-2或0<k<2 | D. | 不存在这样的实数k |
13.掷一个骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“小于4的点数出现”,则一次试验中,事件A+$\overline{B}$发生的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
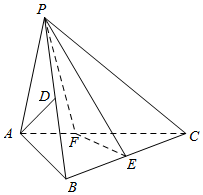 如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.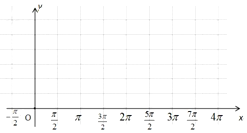 已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$
已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$