题目内容
7.已知集合U={1,2,3,4},B={1,2,3},且A∩B={1,2},则满足条件的A的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据全集U,B,以及A与B的交集,确定出满足条件的A,即可做出判断.
解答 解:∵U={1,2,3,4},B={1,2,3},且A∩B={1,2},
∴满足条件的A可能为{1,2},{1,2,4}共2个,
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
19.2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准,该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值,并从2016年1月1日起在全国实施.空气质量的好坏由空气质量指数确定,空气质量指数越高,代表空气污染越严重,某市对市辖的某两个区加大了对空气质量的治理力度,从2015年11月1日起监测了100天的空气质量指数,并按照空气质量指数划分为:指标小于或等于115为通过,并引进项目投资.大于115为未通过,并进行治理.现统计如下.
(Ⅰ)以频率值作为概率值,求甲区和乙区通过监测的概率;
(Ⅱ)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(Ⅰ)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
| 空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
(Ⅱ)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(Ⅰ)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
16.某企业每天由空气污染造成的经济损失y(单位:元)与空气污染指数API(记为x)的数据统计如下:
(I)求出y与x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(Ⅱ)若该地区某天的空气污染指数为800,预测该企业当天由空气污染造成的经济损失.
附:回归方程中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 空气污染指API(x) | 150 | 200 | 250 | 300 |
| 经济损失y | 200 | 350 | 550 | 800 |
(Ⅱ)若该地区某天的空气污染指数为800,预测该企业当天由空气污染造成的经济损失.
附:回归方程中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
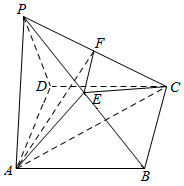 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.