题目内容
17．已知正项数列{an}满足an2-（2n-1）an-2n=0．（1）求数列{an}的通项公式；
（2）记数列{an}的前n项和为Sn，若a1，ak，Sk+2成等比数列，求正整数k．
分析 （1）由已知得（an-2n）（an+1）=0，从而得到an=2n．
（2）{an}是首项为2，公差为2的等差数列，从而Sn=n2+n，由a1，ak，Sk+2成等比数列，得4k2=2[（k+2）2+（k+2）]，由此能求出正整数k．
解答 解：（1）∵正项数列{an}满足an2-（2n-1）an-2n=0．
∴（an-2n）（an+1）=0，
∴an=2n，或an=-1（舍），
∴an=2n．
（2）∵an=2n，∴{an}是首项为2，公差为2的等差数列，
∴Sn=$2n+\frac{n（n-1）}{2}×2$=n2+n，
∵a1，ak，Sk+2成等比数列，
∴${{a}_{k}}^{2}={a}_{1}•{S}_{k+2}$，
∴4k2=2[（k+2）2+（k+2）]，
整理，得k2-5k-6=0，
k=3或k=-2（舍）．
∴正整数k为3．
点评 本题考查数列的通项公式的求法，考查正整数的值的求法，是中档题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．
练习册系列答案
相关题目
5．将函数f（x）=sin（2x+φ）的图象向左平移φ个单位，所得到的函数图象关于y轴对称，则φ的一个可能取值为（ ）
| A． | -$\frac{π}{3}$ | B． | -$\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
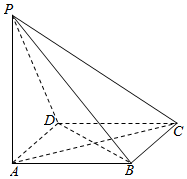如图，四棱锥P-ABCD的底面为正方形，且PA⊥底面ABCD中，AB=1，PA=2．