题目内容
15.若x、y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$,则z=y-$\frac{1}{2}$|x|的最大值为$\frac{5}{2}$.分析 画出约束条件表示的可行域,利用目标函数的几何意义求解最大值即可.
解答 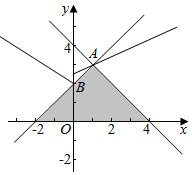 解:$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$表示的可行域如图:z=y-$\frac{1}{2}$|x|,即:y=$\frac{1}{2}|x|$+z=$\left\{\begin{array}{l}{\frac{1}{2}x+z,x≥0}\\{-\frac{1}{2}x+z,x<0}\end{array}\right.$,由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y-4=0}\end{array}\right.$可得,A(1,3),目标函数经过A(1,3)时取得最大值:$\frac{5}{2}$.
解:$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$表示的可行域如图:z=y-$\frac{1}{2}$|x|,即:y=$\frac{1}{2}|x|$+z=$\left\{\begin{array}{l}{\frac{1}{2}x+z,x≥0}\\{-\frac{1}{2}x+z,x<0}\end{array}\right.$,由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y-4=0}\end{array}\right.$可得,A(1,3),目标函数经过A(1,3)时取得最大值:$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查简单线性规划的应用,考查计算能力.

练习册系列答案
相关题目
5.将函数f(x)=sin(2x+φ)的图象向左平移φ个单位,所得到的函数图象关于y轴对称,则φ的一个可能取值为( )
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
3.若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与双曲线$\frac{3{x}^{2}}{{a}^{2}}$-$\frac{3{y}^{2}}{{b}^{2}}$=1共焦点,则双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
10.掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
4.a,b,c,d四名运动员争夺某次赛事的第1,2,3,4名,比赛规则为:通过抽签,将4人分为甲、乙两个小组,每组两人.第一轮比赛(半决赛):两组各自在组内进行一场比赛,决出各组的胜者和负者;第二轮比赛决赛:两组中的胜者进行一场比赛争夺1,2名,两组中的负者进行一场比赛争夺第3,4名.四名选手以往交手的胜负情况累计如下表:
若抽签结果为甲组:a,c;乙组:b,d.每场比赛中,双方以往交手各自获胜的频率作为获胜的概率.
(Ⅰ)求c获得第1名的概率;
(Ⅱ)求c的名次X的分布列和数学期望.
| a | b | c | d | |
| a | a13胜26负 | a20胜10负 | a21胜21负 | |
| b | b26胜13负 | b14胜28负 | b19胜19负 | |
| c | c10胜20负 | c28胜14负 | c18胜18负 | |
| d | d21胜21负 | d19胜19负 | d18胜18负 |
(Ⅰ)求c获得第1名的概率;
(Ⅱ)求c的名次X的分布列和数学期望.
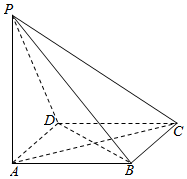 如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2.
如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2. 某商店根据以往某种玩具的销售纪录,绘制了日销售量的频率分布直方图,如图所示.,将日销售量落入各组的频率视为概率,并假设每天的销售量互相独立.
某商店根据以往某种玩具的销售纪录,绘制了日销售量的频率分布直方图,如图所示.,将日销售量落入各组的频率视为概率,并假设每天的销售量互相独立.