题目内容
2.给出下列四个结论:①已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是a=-3b;
②若命题p:?x0∈[1,+∞),x${\;}_{0}^{2}$-x0-1<0,则¬p:?x∈(-∞,1),x2-x-1≥0;
③函数f(x)=sin2x+$\sqrt{3}$cos2x的一条对称轴是x=$\frac{7π}{12}$;
④设回归直线方程为$\widehat{y}$=2-2.5x,当变量x增加一个单位时,y平均增加2个单位.
其中正确结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据直线垂直的等价条件进行判断.
②根据含有量词的命题的否定进行判断.
③根据三角函数的对称性进行判断.
④根据回归直线的性质进行判断.
解答 解:①当b≠0时,两直线的斜率分别为$-\frac{a}{3}$,$-\frac{1}{b}$,由$-\frac{a}{3}$•($-\frac{1}{b}$)=$\frac{a}{3b}$=-1,即a=-3b,
当b=0时,l2:x+1=0,若l1⊥l2,则a=0,此时满足a=-3b,综上l1⊥l2的充要条件是a=-3b;故①正确;
②若命题p:?x0∈[1,+∞),x${\;}_{0}^{2}$-x0-1<0,则¬p:?x∈[1,+∞),x2-x-1≥0;故②错误
③函数f(x)=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
当x=$\frac{7π}{12}$时,f($\frac{7π}{12}$)=2sin(2×$\frac{7π}{12}$+$\frac{π}{3}$)=2sin$\frac{3π}{2}$=-2,为函数的最小值,
则此时函数关于x=$\frac{7π}{12}$对称,故③正确,
④设回归直线方程为$\widehat{y}$=2-2.5x,当变量x增加一个单位时,y平均增加2.5个单位.故④错误,
故正确是①③,
故选:B
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
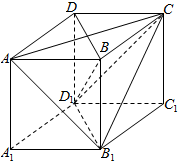 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,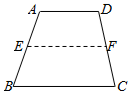 如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.
如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.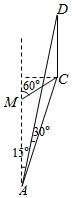 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.