题目内容
18.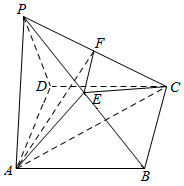 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.(Ⅰ)求证:PC⊥平面AEF;
(Ⅱ)求三棱锥P-AEF的体积.
分析 (1)连结BD,交AC于O,连结OE,由PD∥平面ACE可知OE∥PD,故E为PB中点,从而AE⊥PB,由BC⊥平面PAB可知BC⊥AE,推出AE⊥平面PBC,得到AE⊥PC,结合PC⊥EF,推出PC⊥平面AEF;
(2)由勾股定理求出AE,PB,PC,根据Rt△PEF≌Rt△PCB,列出比例式求出EF,PF,代入体积公式计算.
解答 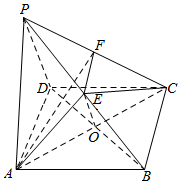 (1)证明连结BD,交AC于O,连结OE,
(1)证明连结BD,交AC于O,连结OE,
∵底面四边形ABCD是正方形,∴O是BD中点.
∵PD∥平面ACE,PD?平面PBD,平面PBD∩平面ACE=OE,
∴PD∥OE,
∴$\frac{BE}{BP}=\frac{BO}{BD}=\frac{1}{2}$,∴E是PB的中点.
∵PA=AB,∴AE⊥PB.
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,又AB⊥BC,PA?平面PAB,AB?平面PAB,PA∩AB=A,
∴BC⊥平面PAB,∵AE?平面PAB,
∴AE⊥BC,又PB?平面PBC,BC?平面PBC,PB∩BC=B,
∴AE⊥平面PBC,∵PC?平面PBC,
∴AE⊥PC,又EF⊥PC,AE?平面AEF,EF?平面AEF,AE∩EF=E,
∴PC⊥平面AEF.
(2)∵PA=AB=1,底面ABCD是正方形,
∴PB=$\sqrt{2}$,AC=$\sqrt{2}$,PC=$\sqrt{3}$,
∴PE=$\frac{\sqrt{2}}{2}$,AE=$\frac{\sqrt{2}}{2}$.
∵Rt△PEF≌Rt△PCB,∴$\frac{PE}{PC}=\frac{PF}{PB}=\frac{EF}{BC}$,∴PF=$\frac{\sqrt{3}}{3}$,EF=$\frac{\sqrt{6}}{6}$.
∴S△AEF=$\frac{1}{2}×AE×EF$=$\frac{\sqrt{3}}{12}$.
∴三棱锥P-AEF的体积V=$\frac{1}{3}{S}_{△AEF}×PF$=$\frac{1}{3}×\frac{\sqrt{3}}{12}×\frac{\sqrt{3}}{3}=\frac{1}{36}$.
点评 本题考查了线面垂直的性质与判定,棱锥的体积计算,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| 组号 | 超速分组 | 频数 | 频率 | 频率 组距 |
| 1 | [0,20%] | 176 | 0.88 | z |
| 2 | [20%,40%] | 12 | 0.06 | 0.0030 |
| 3 | [40%,60%] | 6 | y | 0.0015 |
| 4 | [60%,80%] | 4 | 0.02 | 0.0010 |
| 5 | [80%,100%] | x | 0.01 | 0.0005 |
(2)若在第3,4,5组用分层抽样的方法随机抽取6名驾驶人员做回访调查,并在这6名驾驶员中任选2人进行采访,求这2人中恰有1人超速在[80%,100%]的概率.
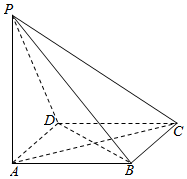 如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2.
如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2.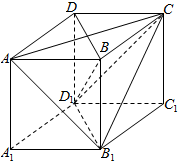 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,