题目内容
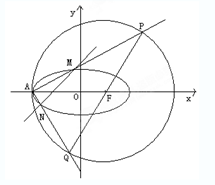 已知A(-2,0)是椭圆C:
已知A(-2,0)是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)过F的直线交圆与P、Q两点,连AP、AQ分别交椭圆与M、N点,试问直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,请说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)a=2,c=1,由此能求出椭圆C的方程.
(2)设直线MN的方程为x=my+t,代入
+
=1,得(3m2+4)y2+6mty+3t2-12=0,由条件得
•
=(x1+2)(x2+2)+y1y2=0,由此能求出直线MN的方程为x=my-
,故直线过定点(-
,0).
(2)设直线MN的方程为x=my+t,代入
| x2 |
| 4 |
| y2 |
| 3 |
| AM |
| AN |
| 2 |
| 7 |
| 2 |
| 7 |
解答:
解:(1)∵A(-2,0)是椭圆C:
+
=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,
且圆心F是椭圆的一个交点,
∴a=2,c=1或c=-5(舍),
∴b2=4-1=3,
∴椭圆C的方程为;
+
=1.
(2)设直线MN的方程为x=my+t,代入
+
=1,
化简,得(3m2+4)y2+6mty+3t2-12=0,
设M(x1,y1),M(x2,y2),则y1+y2=-
,y1y2=
,①
由条件得
•
=(x1+2)(x2+2)+y1y2=0,
即(m2+1)y1y2+m(t+2)y1y2+(t+2)2=0,②
把①代入②,整理,得:
7t2+16t+4=0,解得t=-2,(舍)或t=-
,
∴直线MN的方程为x=my-
,故直线过定点(-
,0).
| x2 |
| a2 |
| y2 |
| b2 |
且圆心F是椭圆的一个交点,
∴a=2,c=1或c=-5(舍),
∴b2=4-1=3,
∴椭圆C的方程为;
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线MN的方程为x=my+t,代入
| x2 |
| 4 |
| y2 |
| 3 |
化简,得(3m2+4)y2+6mty+3t2-12=0,
设M(x1,y1),M(x2,y2),则y1+y2=-
| 6mt |
| 3m2+4 |
| 3t2-12 |
| 3m2+4 |
由条件得
| AM |
| AN |
即(m2+1)y1y2+m(t+2)y1y2+(t+2)2=0,②
把①代入②,整理,得:
7t2+16t+4=0,解得t=-2,(舍)或t=-
| 2 |
| 7 |
∴直线MN的方程为x=my-
| 2 |
| 7 |
| 2 |
| 7 |
点评:本题考查椭圆方程的求法,考查直线方程是否过定点的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
已知函数f(x)=x2+(a-1)x-a为偶函数,则
f(x)dx等于( )
| ∫ | 2 1 |
| A、-1 | ||
B、
| ||
C、
| ||
| D、2 |