题目内容
函数f(x)=x4-2x2-5在[-1,2]上的最小值为 .
考点:二次函数在闭区间上的最值,函数奇偶性的判断
专题:函数的性质及应用
分析:观察解析式,只要利用换元,令t=x2,则原函数等价于f(t)=t2-2t-5,t∈(0,4),明确函数f(t)的单调区间,即可求最小值.
解答:
解:令t=x2,则原函数等价于f(t)=t2-2t-5,t∈(0,4),
f(t)在(0,1)上递减,在[1,4]递增,
∴当t=1时f(t)取最小值为f(1)=1-2-5=-6;
故答案为:-6.
f(t)在(0,1)上递减,在[1,4]递增,
∴当t=1时f(t)取最小值为f(1)=1-2-5=-6;
故答案为:-6.
点评:本题考查了换元法求函数区间的最值问题;本题的关键是将关于x的4次函数通过换元转化为关于t的二次函数求最值;注意换元有时也要换自变量范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数0与集合∅的关系是( )
| A、0∈∅ | B、0=∅ |
| C、0∉∅ | D、{0}=∅ |
设不等式|x-a|<b解集是{x|-1<x<2},则a与b的值是( )
| A、a=1,b=3 | ||||
| B、a=-1,b=3 | ||||
| C、a=-1,b=-3 | ||||
D、a=
|
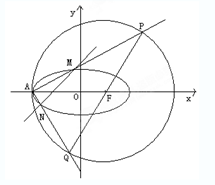 已知A(-2,0)是椭圆C:
已知A(-2,0)是椭圆C: 如图在△ABC中,AC=4,∠ACB=150°,P为△ABC所在平面外一点,PA⊥平面ABC,PA=6,则点P到直线BC的距离为:
如图在△ABC中,AC=4,∠ACB=150°,P为△ABC所在平面外一点,PA⊥平面ABC,PA=6,则点P到直线BC的距离为: