题目内容
满足A⊆{1,2}的集合A的个数为 .
考点:子集与真子集
专题:集合
分析:根据子集的概念,由已知明确集合A中元素可以是0个,1个,2个,由此找到满足条件的集合A.
解答:
解:由题意,满足条件的集合A 有:∅,{1},{2},{1,2}共有4个;
故答案为:4.
故答案为:4.
点评:本题考查了两个集合A,B的关系,要找出A是B的子集的所有集合A,只要使集合A中元素在集合B中,并且A中元素个数≤集合B中元素个数.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
下列各式中,正确的是( )
| A、(z1-z2)2+(z2-z3)2=0?z1=z2=z3 | ||||
B、|z|=1?z=
| ||||
| C、|z1+z2|=|z1|+|z2| | ||||
| D、|z|2=z2 |
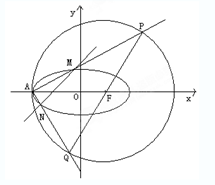 已知A(-2,0)是椭圆C:
已知A(-2,0)是椭圆C: 如图在△ABC中,AC=4,∠ACB=150°,P为△ABC所在平面外一点,PA⊥平面ABC,PA=6,则点P到直线BC的距离为:
如图在△ABC中,AC=4,∠ACB=150°,P为△ABC所在平面外一点,PA⊥平面ABC,PA=6,则点P到直线BC的距离为: