题目内容
已知函数f(x)=aln(x+1),g(x)=x-
x2,a∈R.
(Ⅰ)若a=-1,求曲线y=f(x)在x=3处的切线方程;
(Ⅱ)若对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立,求a的最小值;
(Ⅲ)设p(x)=f(x-1),a>0,若A(x1,y1),B(x2,y2)为曲线y=p(x)的两个不同点,满足0<x1<x2,且?x3∈(x1,x2),使得曲线y=f(x)在x3处的切线与直线AB平行,求证:x3<
.
| 1 |
| 2 |
(Ⅰ)若a=-1,求曲线y=f(x)在x=3处的切线方程;
(Ⅱ)若对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立,求a的最小值;
(Ⅲ)设p(x)=f(x-1),a>0,若A(x1,y1),B(x2,y2)为曲线y=p(x)的两个不同点,满足0<x1<x2,且?x3∈(x1,x2),使得曲线y=f(x)在x3处的切线与直线AB平行,求证:x3<
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(I)当a=-1时,f(x)=-ln(x+1),得出切点(3,-ln4).利用导数的几何意义即可得出切线的斜率,进而得到切线方程;
(II)对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立?aln(x+1)-x+
x2≥0.
令h(x)=aln(x+1)-x+
x2(x≥0).利用导数的运算法则可得h′(x)=
(x≥0).
分类讨论:当a≥1时,当a<1时,只要验证最小值是否大于0即可得出.
(III)p(x)=f(x-1)=alnx,kAB=
.利用导数的运算法则可得p′(x)=
.由于曲线
y=f(x)在x3处的切线与直线AB平行,可得
=
.利用p′(x)在定义域内单调性质要证:x3<
.即证明p′(x3)>p′(
).即证明
>
.变形可得ln
>
=
,
令
=t,则t>1.要证明的不等式等价于lnt>
?(t+1)lnt>2(t-1).构造函数q(t)=(t+1)lnt-2(t-1),(t>1).利用导数研究其单调性即可证明.
(II)对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立?aln(x+1)-x+
| 1 |
| 2 |
令h(x)=aln(x+1)-x+
| 1 |
| 2 |
| x2+a-1 |
| x+1 |
分类讨论:当a≥1时,当a<1时,只要验证最小值是否大于0即可得出.
(III)p(x)=f(x-1)=alnx,kAB=
| alnx2-alnx1 |
| x2-x1 |
| a |
| x |
y=f(x)在x3处的切线与直线AB平行,可得
| alnx2-alnx1 |
| x2-x1 |
| a |
| x3 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| alnx2-alnx1 |
| x2-x1 |
| 2a |
| x1+x2 |
| x2 |
| x1 |
| 2(x2-x1) |
| x2+x1 |
2(
| ||
|
令
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
解答:
解:(I)当a=-1时,f(x)=-ln(x+1),得出切点(3,-ln4).
∵f′(x)=-
,∴切线的斜率k=f′(3)=-
.
∴曲线y=f(x)在x=3处的切线方程为:y+ln4=-
(x-3),化为x+4y+8ln2-3=0.
(II)对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立?aln(x+1)-x+
x2≥0.
令h(x)=aln(x+1)-x+
x2(x≥0).
h′(x)=
-1+x=
(x≥0).
①当a≥1时,h′(x)≥0恒成立,
∴函数h(x)在x∈[0,+∞)上单调递增,∴h(x)≥h(0)=0,∴a≥1时符合条件.
②当a<1时,由h′(x)=0,及x≥0,解得x=
.
当x∈(0,
)时,h′(x)<0;当x∈(
,+∞)时,h′(x)>0.
∴hmin(x)=h(
)=h(
)<h(1)=0,这与h(x)≥0相矛盾,应舍去.
综上可知:a≥1.∴a的最小值为1.
(III)p(x)=f(x-1)=alnx,kAB=
.
∵p′(x)=
,∴p′(x3)=
.
∵曲线y=f(x)在x3处的切线与直线AB平行,
∴
=
.
由p′(x)=
,a>0,可知其在定义域内单调递减.
要证:x3<
.即证明p′(x3)>p′(
).即证明
>
.
变形可得ln
>
=
,
令
=t,则t>1.要证明的不等式等价于lnt>
?(t+1)lnt>2(t-1).
构造函数q(t)=(t+1)lnt-2(t-1),(t>1).
q′(x)=lnt+
-2=lnt+
-1(t>1).
令u(t)lnt+
-1,(t>1).
则u′(t)=
-
=
>0,∴q′(t)在t>1时单调递增.
∴q′(t)>q′(1)=0,∴函数q(t)在区间(1,+∞)上单调递增,∴q(t)>q(1)=0,
∴q(t)>0在(1,+∞)上恒成立.
∴(t+1)lnt>2(t-1)在(1,+∞)上恒成立,即x3<
成立.
∵f′(x)=-
| 1 |
| x+1 |
| 1 |
| 4 |
∴曲线y=f(x)在x=3处的切线方程为:y+ln4=-
| 1 |
| 4 |
(II)对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立?aln(x+1)-x+
| 1 |
| 2 |
令h(x)=aln(x+1)-x+
| 1 |
| 2 |
h′(x)=
| a |
| x+1 |
| x2+a-1 |
| x+1 |
①当a≥1时,h′(x)≥0恒成立,
∴函数h(x)在x∈[0,+∞)上单调递增,∴h(x)≥h(0)=0,∴a≥1时符合条件.
②当a<1时,由h′(x)=0,及x≥0,解得x=
| 1-a |
当x∈(0,
| 1-a |
| 1-a |
∴hmin(x)=h(
| 1-a |
| 1-a |
综上可知:a≥1.∴a的最小值为1.
(III)p(x)=f(x-1)=alnx,kAB=
| alnx2-alnx1 |
| x2-x1 |
∵p′(x)=
| a |
| x |
| a |
| x3 |
∵曲线y=f(x)在x3处的切线与直线AB平行,
∴
| alnx2-alnx1 |
| x2-x1 |
| a |
| x3 |
由p′(x)=
| a |
| x |
要证:x3<
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| alnx2-alnx1 |
| x2-x1 |
| 2a |
| x1+x2 |
变形可得ln
| x2 |
| x1 |
| 2(x2-x1) |
| x2+x1 |
2(
| ||
|
令
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
构造函数q(t)=(t+1)lnt-2(t-1),(t>1).
q′(x)=lnt+
| t+1 |
| t |
| 1 |
| t |
令u(t)lnt+
| 1 |
| t |
则u′(t)=
| 1 |
| t |
| 1 |
| t2 |
| t-1 |
| t2 |
∴q′(t)>q′(1)=0,∴函数q(t)在区间(1,+∞)上单调递增,∴q(t)>q(1)=0,
∴q(t)>0在(1,+∞)上恒成立.
∴(t+1)lnt>2(t-1)在(1,+∞)上恒成立,即x3<
| x1+x2 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、构造函数法、换元法、恒成立问题的等价转化、分类讨论等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
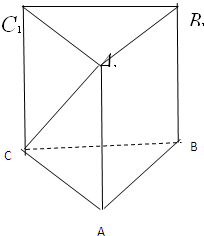 如图三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,
如图三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,