题目内容
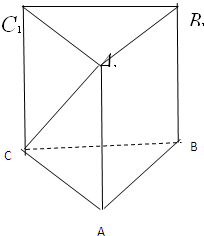如图三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°，证明：AB⊥A1C．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：取AB的中点O，连接OC，OA1，A1B，利用已知条件，先证明AB⊥平面OA1C，由此能够证明AB⊥A1C．
解答：
证明：取AB的中点O，连接OC，OA1，A1B，
∵CA=CB，
∴OC⊥AB，
又∵AB=AA1，∠BAA1=60°，
∴△AA1B是等边三角形，
∴OA1⊥AB，
∵OC∩OA1=O，
∴AB⊥平面OA1C，
∵A1C?平面OA1C，
∴AB⊥A1C．
证明：取AB的中点O，连接OC，OA1，A1B，∵CA=CB，
∴OC⊥AB，
又∵AB=AA1，∠BAA1=60°，
∴△AA1B是等边三角形，
∴OA1⊥AB，
∵OC∩OA1=O，
∴AB⊥平面OA1C，
∵A1C?平面OA1C，
∴AB⊥A1C．
点评：本题考查异面直线垂直的证明，解题时要注意空间思维能力的培养，注意化空间问题为平面问题．
练习册系列答案
名校课堂系列答案
相关题目
