题目内容
已知直线l:(2m+1)x+(m+1)y=7m+4,圆C:(x-1)2+(y-2)2=25
(1)求直线l经过的定点坐标;
(2)求证:直线l与圆C总相交(提示:只需证明直线l经过圆内的一点);
(3)求出相交弦长的最小值及对应的m值.
(1)求直线l经过的定点坐标;
(2)求证:直线l与圆C总相交(提示:只需证明直线l经过圆内的一点);
(3)求出相交弦长的最小值及对应的m值.
考点:直线和圆的方程的应用
专题:计算题,证明题,直线与圆
分析:(1)将直线化简为(2x+y-7)m+(x+y-4)=0,然后令2x+y-7=0,x+y-4=0,解方程组即可得到定点坐标;
(2)由(1)得,直线l过定点A(3,1),求出AC的距离,与圆的半径半径,说明A在圆内,即可得证;
(3)直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l,求出CA的斜率,可得l的斜率,从而可求m的值,求出弦心距,可得直线l被圆C截得的弦长的最小值.
(2)由(1)得,直线l过定点A(3,1),求出AC的距离,与圆的半径半径,说明A在圆内,即可得证;
(3)直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l,求出CA的斜率,可得l的斜率,从而可求m的值,求出弦心距,可得直线l被圆C截得的弦长的最小值.
解答:
(1)解:由直线l:(2m+1)x+(m+1)y-7m-4=0
可得(2x+y-7)m+(x+y-4)=0
对于任意实数m,要使上式成立,必须
,
解得:
所以直线l过定点A(3,1);
(2)证明:由(1)得,直线l过定点A(3,1),
圆C:(x-1)2+(y-2)2=25圆心为C(1,2),半径为5.
|AC|=
=
<5,即有A在圆内,
则有直线l与圆C总相交;
(3)解:直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l,
∵圆C:(x-1)2+(y-2)2=25,圆心(1,2),半径为5
∴CA的斜率为
=-
,
∴l的斜率为2,
∵直线l:(2m+1)x+(m+1)y-7m-4=0的斜率为-
,
∴-
=2,
∴m=-
,
∵|CA|=
=
,
∴直线l被圆C截得的弦长的最小值为2
=4
.
则相交弦长的最小值是4
,对应的m=-
.
可得(2x+y-7)m+(x+y-4)=0
对于任意实数m,要使上式成立,必须
|
解得:
|
所以直线l过定点A(3,1);
(2)证明:由(1)得,直线l过定点A(3,1),
圆C:(x-1)2+(y-2)2=25圆心为C(1,2),半径为5.
|AC|=
| (3-1)2+(1-2)2 |
| 5 |
则有直线l与圆C总相交;
(3)解:直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l,
∵圆C:(x-1)2+(y-2)2=25,圆心(1,2),半径为5
∴CA的斜率为
| 2-1 |
| 1-3 |
| 1 |
| 2 |
∴l的斜率为2,
∵直线l:(2m+1)x+(m+1)y-7m-4=0的斜率为-
| 2m+1 |
| m+1 |
∴-
| 2m+1 |
| m+1 |
∴m=-
| 3 |
| 4 |
∵|CA|=
| 4+1 |
| 5 |
∴直线l被圆C截得的弦长的最小值为2
| 25-5 |
| 5 |
则相交弦长的最小值是4
| 5 |
| 3 |
| 4 |
点评:本题考查直线恒过定点,考查直线和圆的位置关系及弦长的计算,解题的关键是掌握圆的特殊性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
平面向量
,
满足|3
•
|≤4,则向量
•
的最小值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
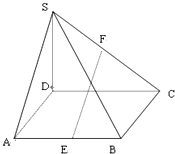 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3. 正四棱锥P-ABCD的所有棱长均相等,E是PC的中点,那么异面直线BE与PA所成的角的余弦值等于
正四棱锥P-ABCD的所有棱长均相等,E是PC的中点,那么异面直线BE与PA所成的角的余弦值等于