题目内容
6.设$f(x)={x^3}+{log_2}(x+\sqrt{{x^2}+1})$,则对任意实数a、b,若a+b≥0则( )| A. | f(a)+f(b)≤0 | B. | f(a)+f(b)≥0 | C. | f(a)-f(b)≤0 | D. | f(a)-f(b)≥0 |
分析 求解函数f(x)的定义域,判断其奇偶性和单调性,利用奇偶性和单调性可得答案.
解答 解:设$f(x)={x^3}+{log_2}(x+\sqrt{{x^2}+1})$,其定义域为R,
$f(-x)={-x^3}+{log_2}(-x+\sqrt{{x^2}+1})$=$-{x}^{3}-lo{g}_{2}(x+\sqrt{{x}^{2}+1})$=-f(x),
∴函数f(x)是奇函数.且在(0,+∞)上单调递增,
故函数f(x)在R上是单调递增,
那么:a+b≥0,即a≥-b,
∴f(a)≥f(-b),
得f(a)≥-f(b),
可得:f(a)+f(b)≥0.
故选:B.
点评 本题考查了函数的奇偶性和单调性的判断及其运用能力.属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
16.“m<0”是“$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{m-1}$=1表示的曲线是双曲线”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.如果偶函数在[a,b]具有最大值,那么该函数在[-b.-a]有( )
| A. | 最大值 | B. | 最小值 | C. | 没有最大值 | D. | 没有最小值 |
14.某企业节能降耗技术改造后,在生产某产品过程中几录的产量x(吨)与相应的生产能耗y(吨)的几
组对应数据如表所示:
若根据表中数据得出y关于x的线性回归方程为$\stackrel{∧}{y}$=0.7x+0.35,则表中a的值为( )
组对应数据如表所示:
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | a |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
18.已知双曲线$E:{x^2}-\frac{y^2}{3}=1$的左焦点为F,直线x=2与双曲线E相交于A,B两点,则△ABF的面积为( )
| A. | 12 | B. | 24 | C. | $4\sqrt{3}$ | D. | $8\sqrt{3}$ |
16.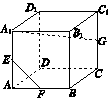 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |